Michelson II | Sagnac

The Michelson interferometer - relativistic!

Here again the sketches of the dynamics of the (Light) signal (red arrow): the Superposition of a movement with the speedt v (black arrow) gives the resulting movement "c.dt" (red dashed arrow). (s.d.here)

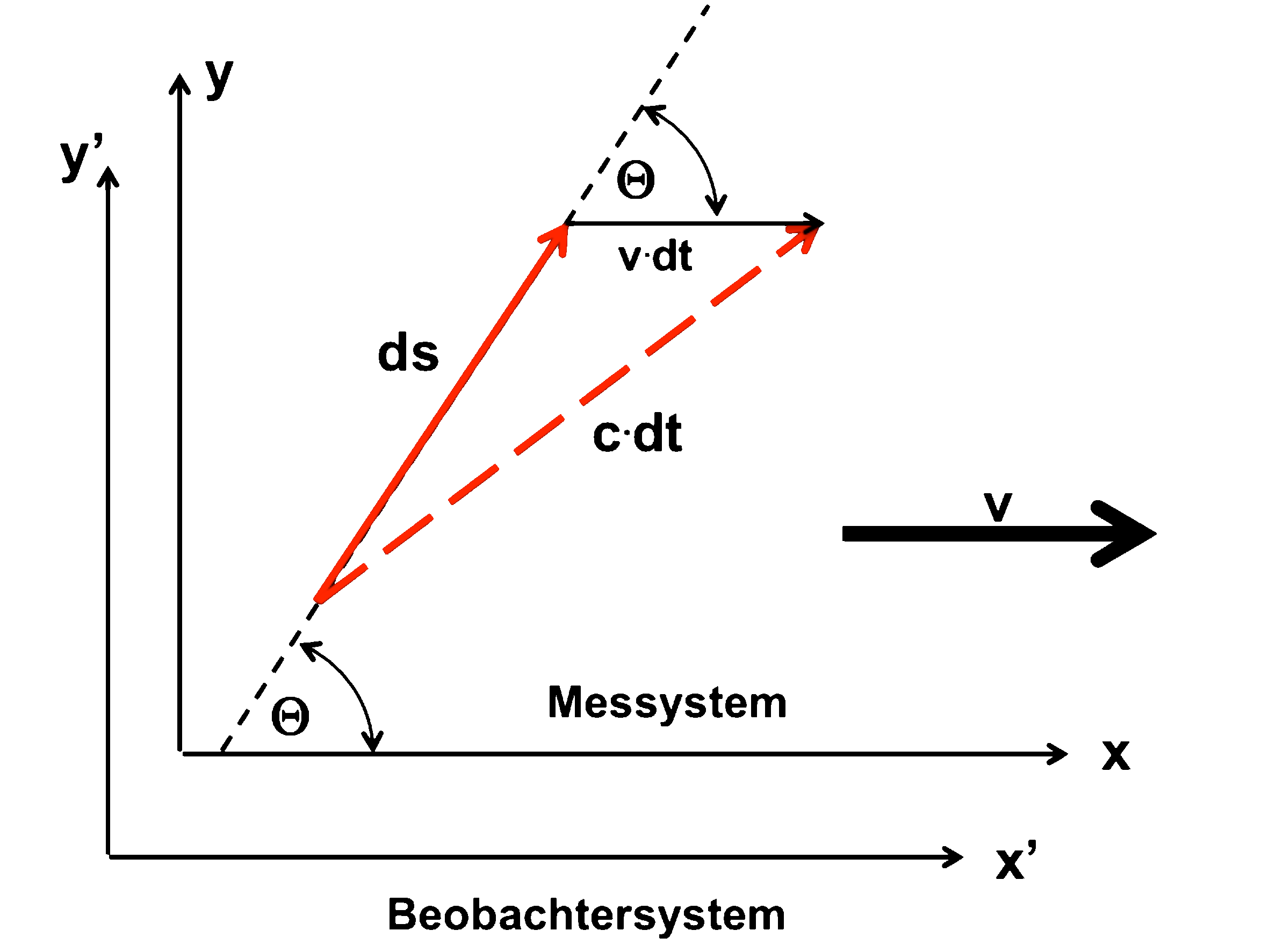
"There"

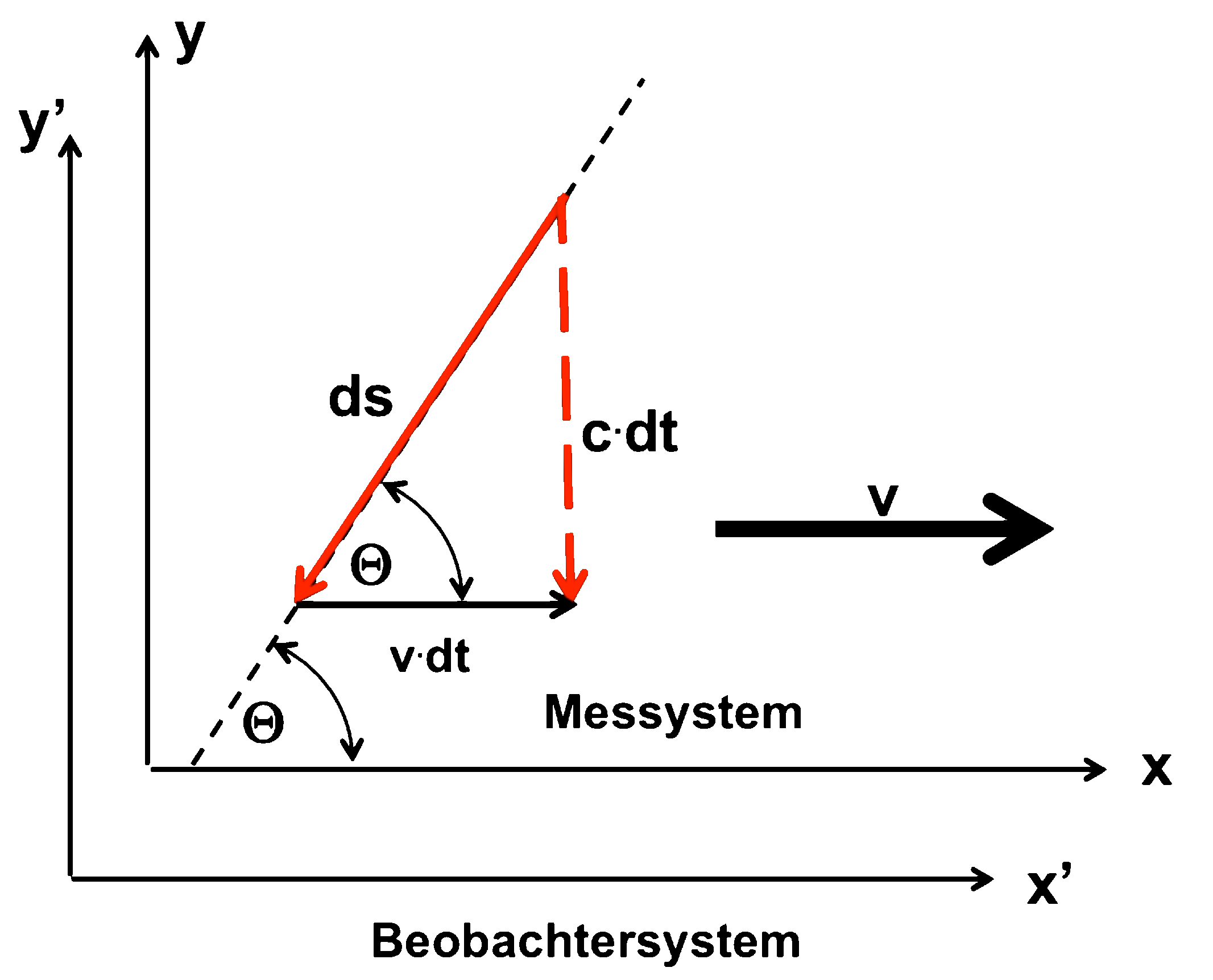
"way back"

with:

dt' - signal propagation time in the distance element ds
ds - distance element
c' - signal velocity
v - velocity of the path element relative to the observer;

with cO vacuum speed of light;

angle between ds and v ;

In the chapter "Solution - runtime effects in relatively moving systems" we have derived a formula that allows us to calculate the runtime of a (light) signal over a distance element ds.

You remember ? (Here you can do everything again read !)

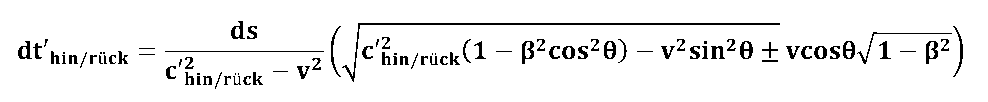
When deriving this formula, a stationary observer and a moving measuring system (light guide) were assumed.

The "deleted" sizes refer to the stationary observer system; Unprimed sizes refer to the moving measuring system.

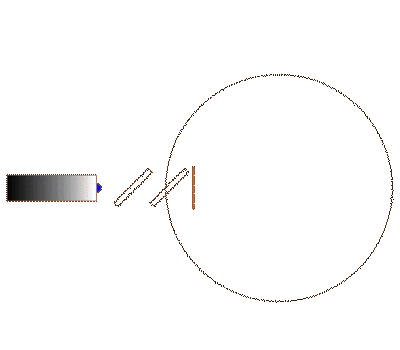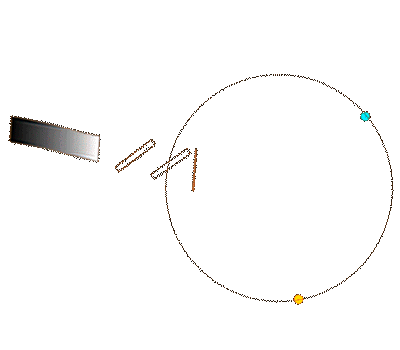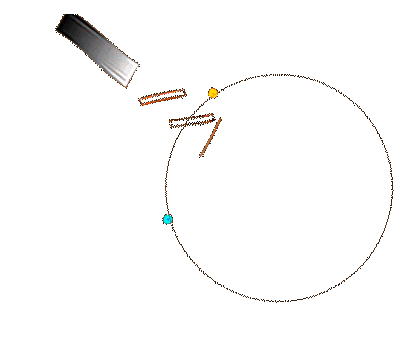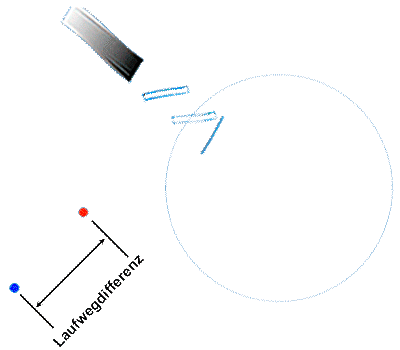
Sagnac measuring principle: Runtime difference between the signals circulating in opposite directions.

With the above formula it should now be possible to describe the effects observed at the Sagnac and Michelson interferometers without contradiction. At the Sagnac interferometer we are dealing with a rotating system, i.e. there is basically a "resting" observer and a relatively moving light guide system (more details here!)

For the Sagnac interferometers with wave trains rotating in opposite directions, the measuring effect results from the difference in the travel times for the outward and return journeys. (more here.)

dt'sagnac = dt'there - dt'return

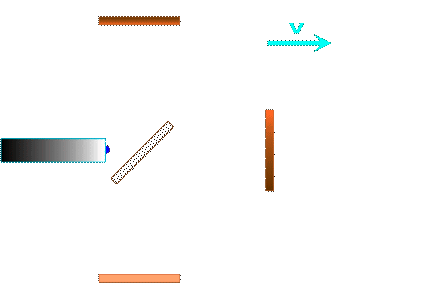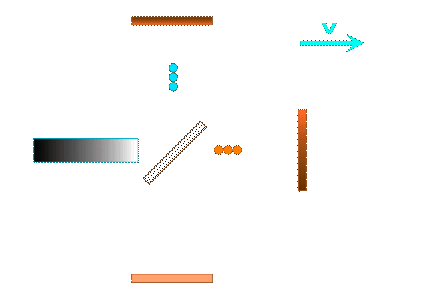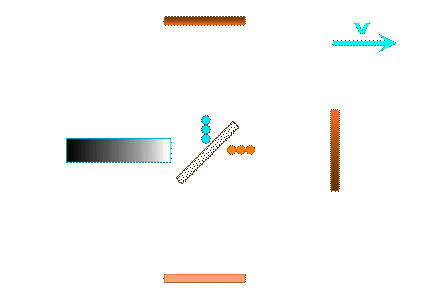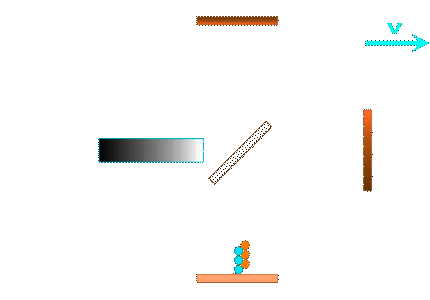
Michelson-chain-in-movement-with-frames_450x300pt-new.gif

For the Michelson interferometer we have to form the sum of the travel times for the outward and return journey in each of the two arms: (more here) and then compare the transit times in both interferometer arms:

dt'Michelson = dt'there + dt'return

Michelson measurement principle: Transit time (back and forth) in the interferometer arm parallel to the direction of movement / transit time difference between to the poor.

Calculation of the transit time effect in the Michelson interferometer

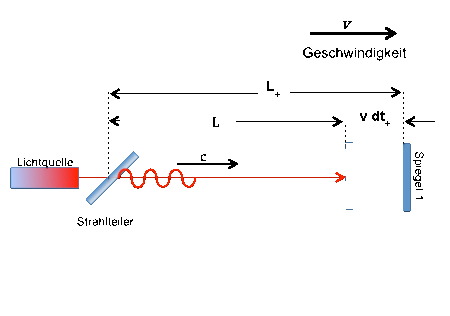
Here is the basic sketch for one arm of the Michelson interferometer:

First of all we will simplify the above formula for the signal propagation time a bit, without restricting the generality. Since we are planning a runtime experiment with a light beam, we use the vacuum light speed c0 as the signal speed c' for the outward and return path!

With c' = c0, the running time for the outward journey results from the above formula:

And for the way back:

In a Michelson interferometer we now have to add the transit times for the outward and return journeys (more on this), i.e. for the total transit time in an interferometer arm, (dt'Michelson = dt'hin + dt'back )

with:

Notice what?

The expression for the runtime dt'Michelson ( way there + way back !) no longer contains the angle between the direction of signal propagation and the direction of movement of the measuring system.

I.e. you can turn the interferometer as you like, there will be no runtime change!

We have shown that when applying the relativistic coordinate transformationalso one oppositemoving Interferometer stationary observer no runtime effect can register !

The one with the Michelson interferometermore moved observer does not show any runtime / measurement effect is actually not further surprising. We know since the "dialogue" from the year 1630 by Galileo Gallilei (1564-1642) that in a closed system there is no possibility of registering a uniform movement. (Please also remember thatFall experiment in the railway car !)

But: during the discussion ofMichelson interferometer were we about the questionstumbled why one opposite the deviceresting observer also no measurement effect registered. We had to leave this question open for the time being, it was from the point of view of classical / pre-relativistic physics cannot be answered! (Please scroll back again!) - With the derivation shown here, however, it becomes clear that this negative result is a result ofrelativistic properties of light.

AA Michelson's search for an "ether" as a carrier medium for light was therefore -despite the zero result - successful in two respects:

1. The fact that the observer moving with the experiment - i.e. the original "Michelson configuration" - could not determine any measuring effect, suggests that there is no "ether" for the light or electromagnetic waves exists, at least not in the sense of a carrier medium such as air for sound.

2. The fact that the observer who is stationary in relation to the interferometer also has no measurement effect registered, cannot be explained within the framework of classical physics and is therefore, among other things, the starting point for the special theory of relativity.

Here's another important note: We have discussed the (relativistic) Michelson effect broken off at the point where it became clear that when the device was rotated - as Michelson intended - no walking distance effect was to be expected and the interferometer thus basically could not deliver any result. (go againback !) For a complete relativistic description of the Michelson interferometer, one would of course also have to consider the signal velocity c' if they differ from the vacuum speed of light should be c0 (!), have to correct relativistically. We will not be spared this when deriving the Sagnac effect: the result is but surprised !