
Sagnac, Michelson & Co
Relativität zum "Anfassen"
Rüdiger Rodloff
Hintergrundbild - DLR - Experimental-Laserkreisel - ELSY
Das Michelson-Interferometer - relativistisch !
Hier noch einmal die Skizzen zur Dynamik des (Licht-)Signals (roter Pfeil) : die Überlagerung einer Bewegung mit der Geschwindigkeit v (schwarzer Pfeil) ergibt die resultierende Bewegung "c.dt" (roter gestrichelter Pfeil). (s.d. hier)
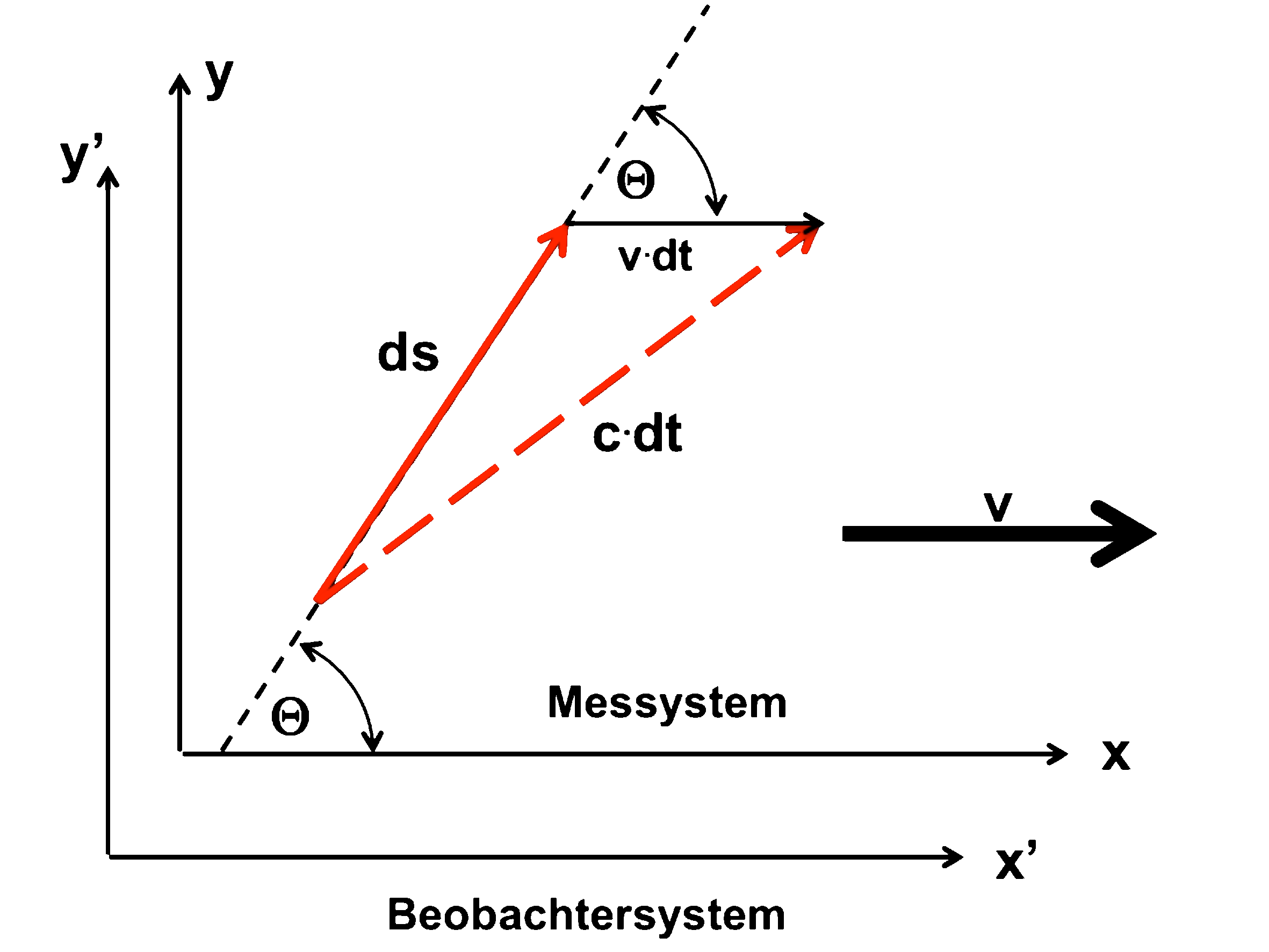
"Hinweg"
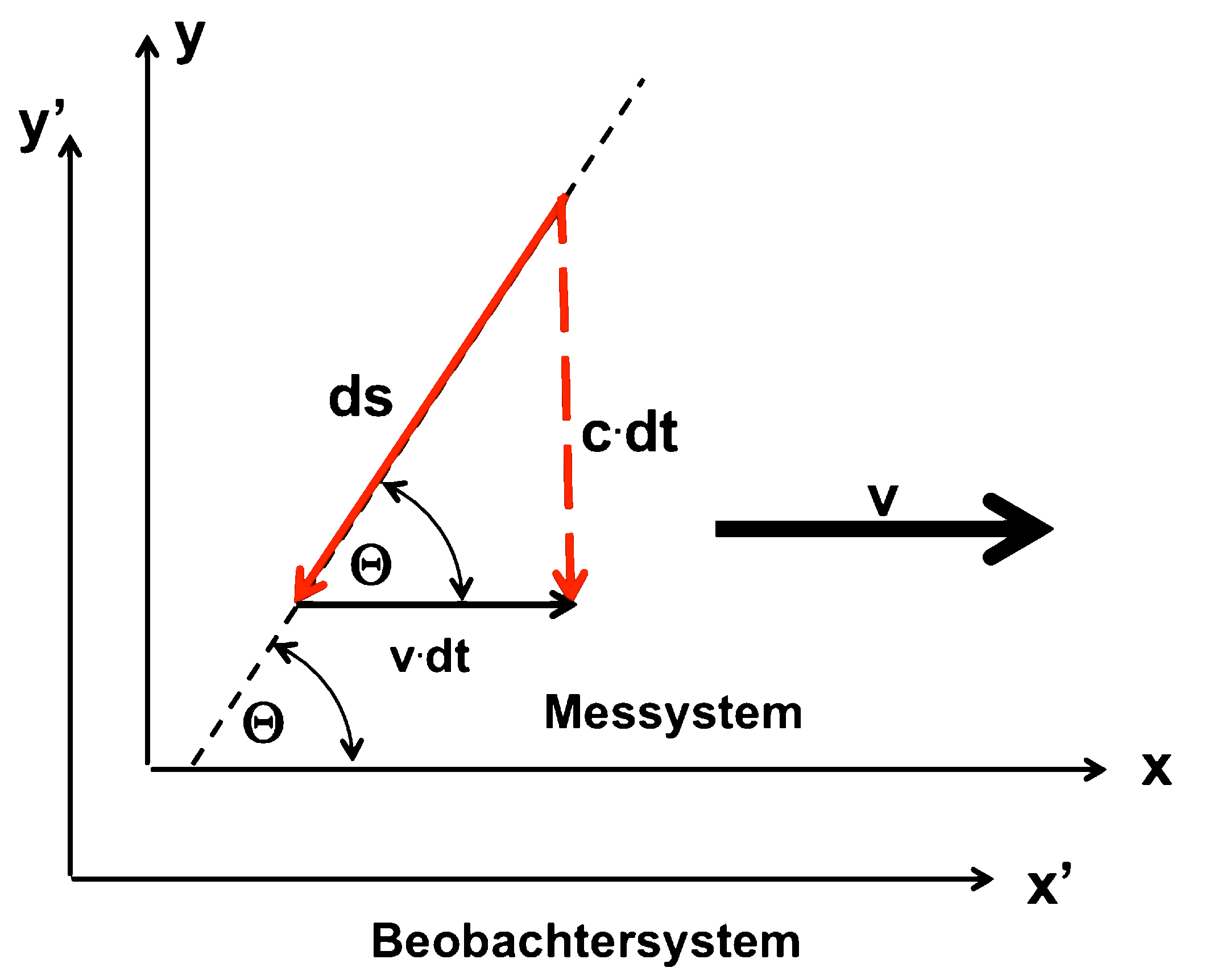
"Rückweg"
mit:
dt' - Signallaufzeit im Wegstreckenelement ds
ds - Wegstreckenelement
c' - Signalgeschwindigkeit
v - Geschwindigkeit des Wegstreckenelementes relativ zum Beobachter;
mit co Vakuumlichtgeschwindigkeit;
Winkel zw. ds und v ;
Wir haben im Kapitel "Lösung - Laufzeiteffekte in relativ bewegten Systemen " eine Formel hergeleitet, die es uns erlaubt die Laufzeit eines (Licht-)Signals über ein Wegstreckenelement ds zu berechnen.
Sie erinnern sich ? (Hier können Sie alles auch noch einmal nachlesen ! )
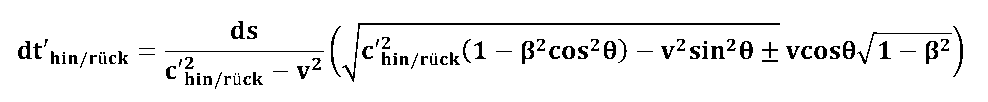
Bei der Herleitung dieser Formel wurde ein ruhender Beobachter und ein bewegtes Messystem (Lichtleiter) vorausgesetzt.
Die "gestrichenen" Größen beziehen sich auf das ruhende Beobachtersystem; ungestrichene Gößen beziehen sich auf das bewegte Messystem.
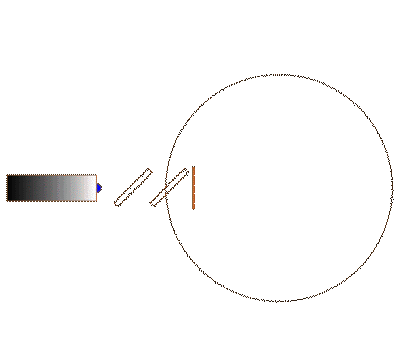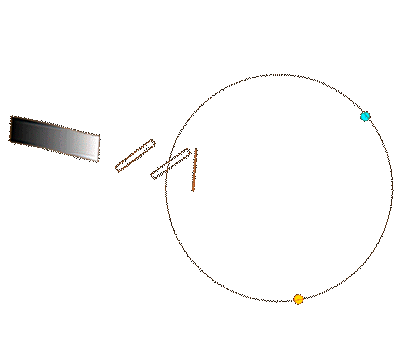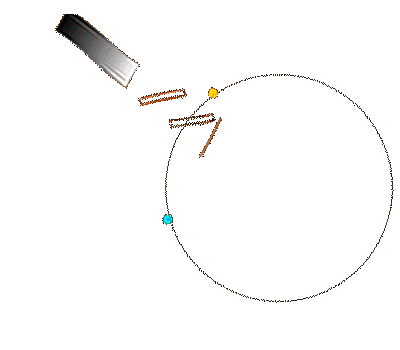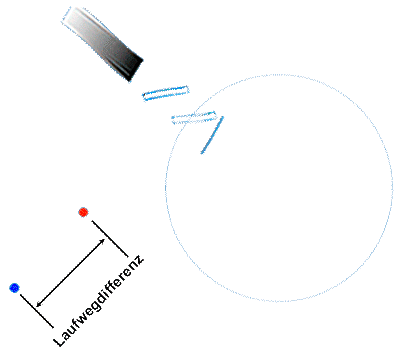
Sagnac-Messprinzip: Laufzeitdifferenz zwischen den gegensinnig umlaufenden Signalen.
Mit obigen Formel sollte es jetzt möglich sein, die am Sagnac- und am Michelson-Interferometer beobachteten Effekte widerspruchsfrei zu beschreiben. Beim Sagnac-Interferometer haben wir es mit einem rotierenden System zu tun, d.h. es gibt grundsätzlich einen "ruhenden" Beobachter und ein dazu relativ bewegtes Lichtleitsystem (weitere Einzelheiten hier !)
Für die im Sagnac-Interferometer gegensinnig umlaufenden Wellenzüge ergibt sich der Messeffekt aus der Differenz der Laufzeiten für Hin- und Rückweg. (mehr dazu hier.)
dt'Sagnac = dt'hin - dt'rück
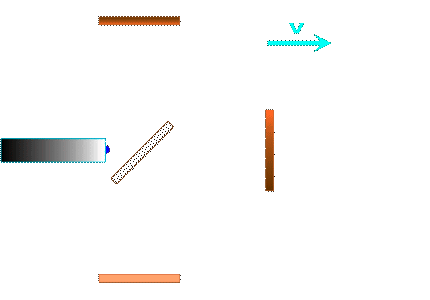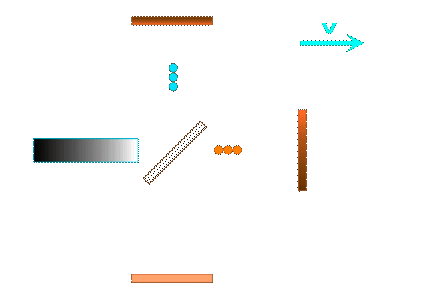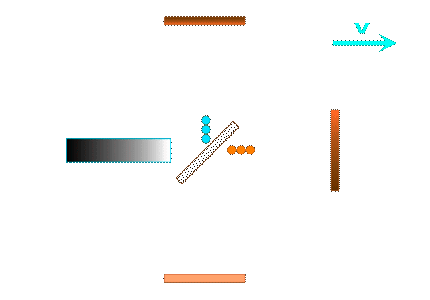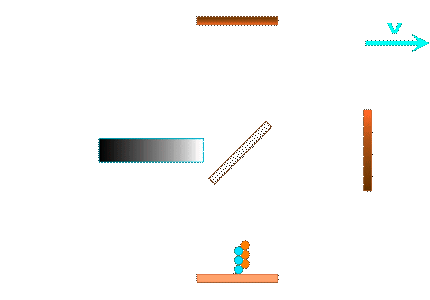
Für das Michelson-Inferometer müssen wir in jedem der beiden Arme jeweils die Summe der Laufzeiten für Hin- und Rückweg bilden: (mehr dazu hier) und anschliessend die Laufzeiten in beiden Interferometerarmen vergleichen:
dt'Michelson = dt'hin + dt'rück
Michelson-Messprinzip: Laufzeit (hin und rück) im Interferometerarm parallel zur Bewegungsrichtung / Laufzeitdifferenz zwischen den Armen.
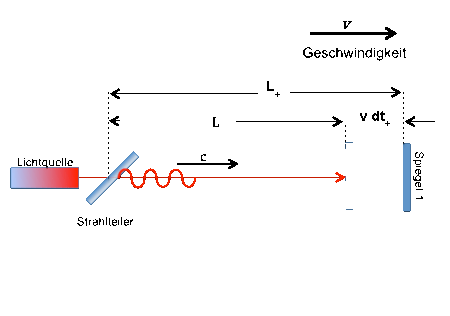
Berechnung des Laufzeiteffektes im Michelson-Interferometer
Hier noch einmal die Prinzipskizze für einen Arm des Michelson-Interferometers:
Zunächst 'mal werden wir die obige Formel für die Signallaufzeit etwas vereinfachen, ohne dabei die Allgemeingültigkeit einzuschränken. Da wir ein Laufzeitexperiment mit einem Lichtstrahl vorhaben, setzen wir als Signalgeschwindigkeit c' für den Hin- und Rückweg die Vakuumlichtgeschwindigkeit c0 an !
Als Laufzeit für den Hinweg ergibt sich mit c' = c0 aus der obigen Formel:
Und für den Rückweg gilt:
In einem Michelsoninterferometer müssen wir nun die Laufzeiten für Hin- und Rückweg addieren (mehr dazu), d.h. wir erhalten für die Gesamtlaufzeit in einem Interferometerarm, (dt'Michelson = dt'hin + dt'rück )
mit:




Merken Sie was ?
Der Ausdruck für die Laufzeit dt'Michelson ( Hinweg + Rückweg !) enthält nicht mehr den Winkel zwischen der Signallaufrichtung und der Bewegungsrichtung des Messystems.
D.h. Sie können das Interferometer drehen wie Sie wollen, es wird keine Laufzeitänderung auftreten!
Wir haben damit gezeigt, daß bei Anwendung der relativistischen Koordinatentransformation auch ein gegenüber dem bewegten Interferometer ruhender Beobachter keinen Laufzeiteffekt registrieren kann !
Das ein mit dem Michelson-Inferometer mitbewegter Beobachter keinem Laufzeit-/ Messeffekt zeigt, ist eigentlich nicht weiter verwunderlich. Wissen wir doch seit dem "Dialogo" aus dem Jahr 1630 von Galileo Gallilei (1564-1642), dass es in einem abgeschlossenen System keine Möglichkeit gibt, eine gleichförmige Bewegung zu registrieren. (Erinnern Sie sich bitte auch an das Fallexperiment im Eisenbahnwagen !)
Aber: bei der Diskussion des Michelson- Interferometers waren wir über die Frage gestolpert warum ein gegenüber dem Gerät ruhender Beobachter ebenfalls keinen Messeffekt registriert. Wir mussten diese Frage zunächst offen lassen, sie war aus der Sicht der klassischen / vorrelativistischen Physik nicht zu beantworten ! (Blättern Sie bitte nochmal zurück !) - Mit der hier gezeigten Herleitung wird aber klar, das dieses Negativergebnis ein Resultat der relativistischen Eigenschaften des Lichtes ist.
Die Suche von A.A. Michelson nach einem "Äther" als Trägermedium des Lichtes, war deshalb - trotz des Nullresultates - in doppelter Hinsicht erfolgreich:
1. Die Tatsache, dass der mit dem Experiment mitbewegte Beobachter - also die ursprüngliche "Michelson-Konfiguration" - keinen Messeffekt feststellen konnte, lässt darauf schliessen, dass es keinen "Äther" für das Licht bzw. elektromagnetische Wellen gibt, zumindest nicht im Sinne eines Trägermediums wie z.B. die Luft für den Schall.
2. Die Tatsache, dass auch der gegenüber dem Interferometer ruhende Beobachter keinen Messeffekt registriert, ist im Rahmen der klassischen Physik nicht erklärbar und ist damit u.a. der Ausgangspunkt für die spezielle Relativitätstheorie.
Hier noch eine wichtige Anmerkung: Wir haben die Diskussion des (relativistischen) Michelsoneffektes an der Stelle abgebrochen, an der deutlich wurde, dass bei einer Verschwenkung des Gerätes - so wie Michelson das beabsichtigte - kein Laufwegseffekt zu erwarten war und das Interferometer damit grundsätzlich auch kein Ergebnis lieferen konnte. (gehen Sie doch nochmal zurück !) Für eine vollständige relativistische Beschreibung des Michelson-Interferometers hätte man natürlich auch noch die Signalgeschwindigkeit c' , wenn sie unterschiedlich von der Vakuum-Lichtgeschwindigkeit c0 sein solle (!), relativistisch korrigieren müssen. Bei der Herleitung des Sagnaceffektes wird uns das nicht erspart bleiben: das Ergebnis ist aber überraschend !