
Sagnac, Michelson & Co
Relativity to "touch"
RuedigerRodloff
Background image - DLR - Experimental Laser Gyro - ELSY
The Sagnac interferometer - relativistic!
with:
dt' - signal propagation time in the distance element ds
ds - distance element
c' - signal velocity
v - velocity of the path element relative to the observer;
with c0 vacuum speed of light;
angle between ds and v ;
A Sagnac interferometer can be constructed in very different ways, -
but basically a self-contained guidance system for the signal or the light waves is always required
This can be realized with deflection mirrors, prisms or optical waveguides or glass fibers. In particular, the "glass fiber gyroscope" is of great practical importance and it is therefore also of interest in which way the temperature-dependent refractive index or the signal speed influences the measuring effect.
To put it bluntly - if it turns out that the measuring effect of the "fiber gyroscope" depends on the speed of light or the refractive index and is therefore temperature-sensitive, then we have a (technical) problem!
Well, then let's see:
We have in the chapter "Solution - Runtime effects in relatively moving systems" derived a formula that allows us to calculate the transit time of a (light) signal over a path element ds in motion. (Here's the runtime formula!)
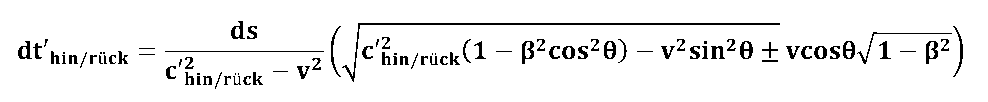
The "deleted" sizes refer to the stationary observer system; Unprimed sizes refer to the moving measuring system.
You remember ? (You can do it all again here read ! )
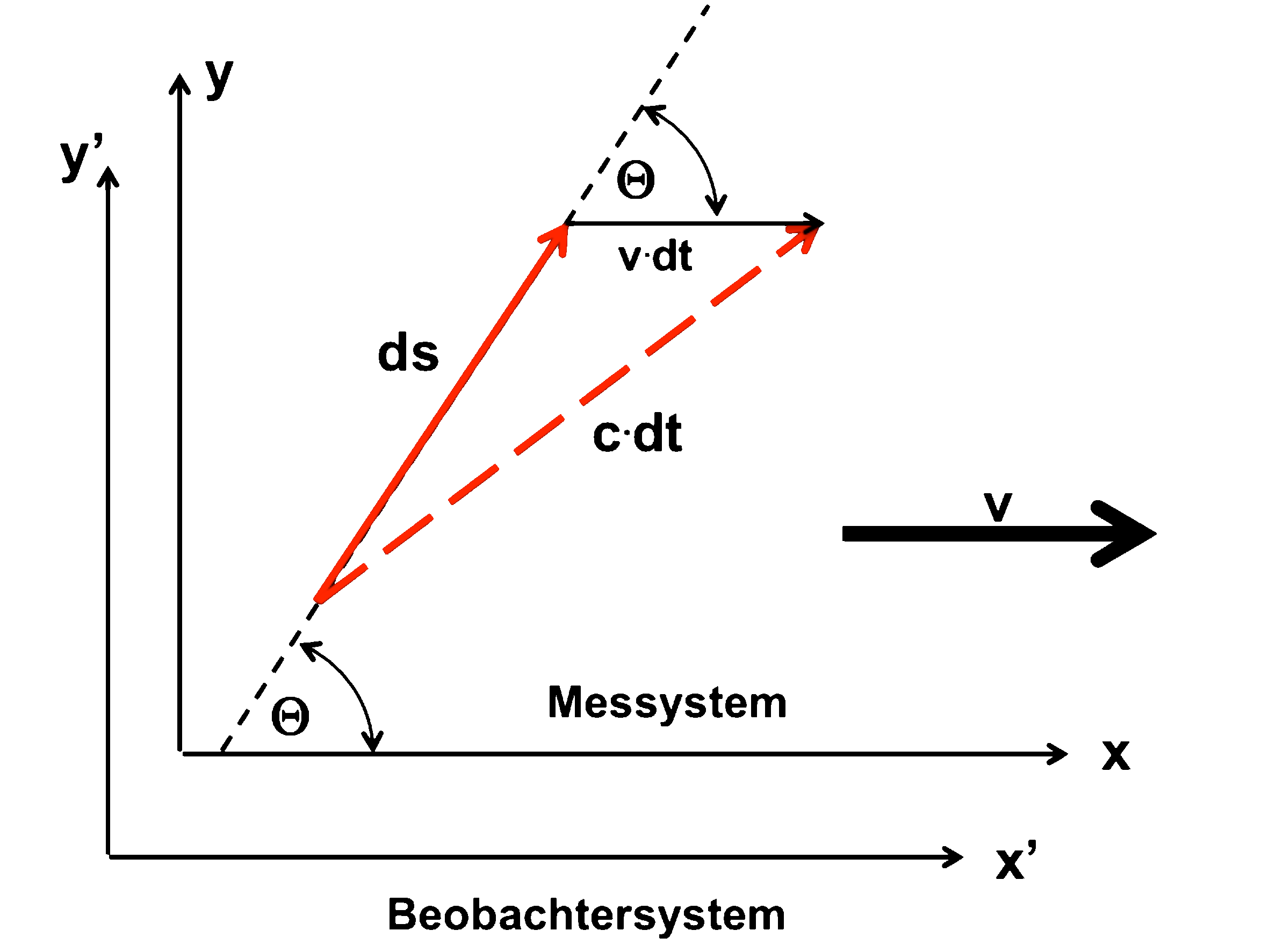
"there"
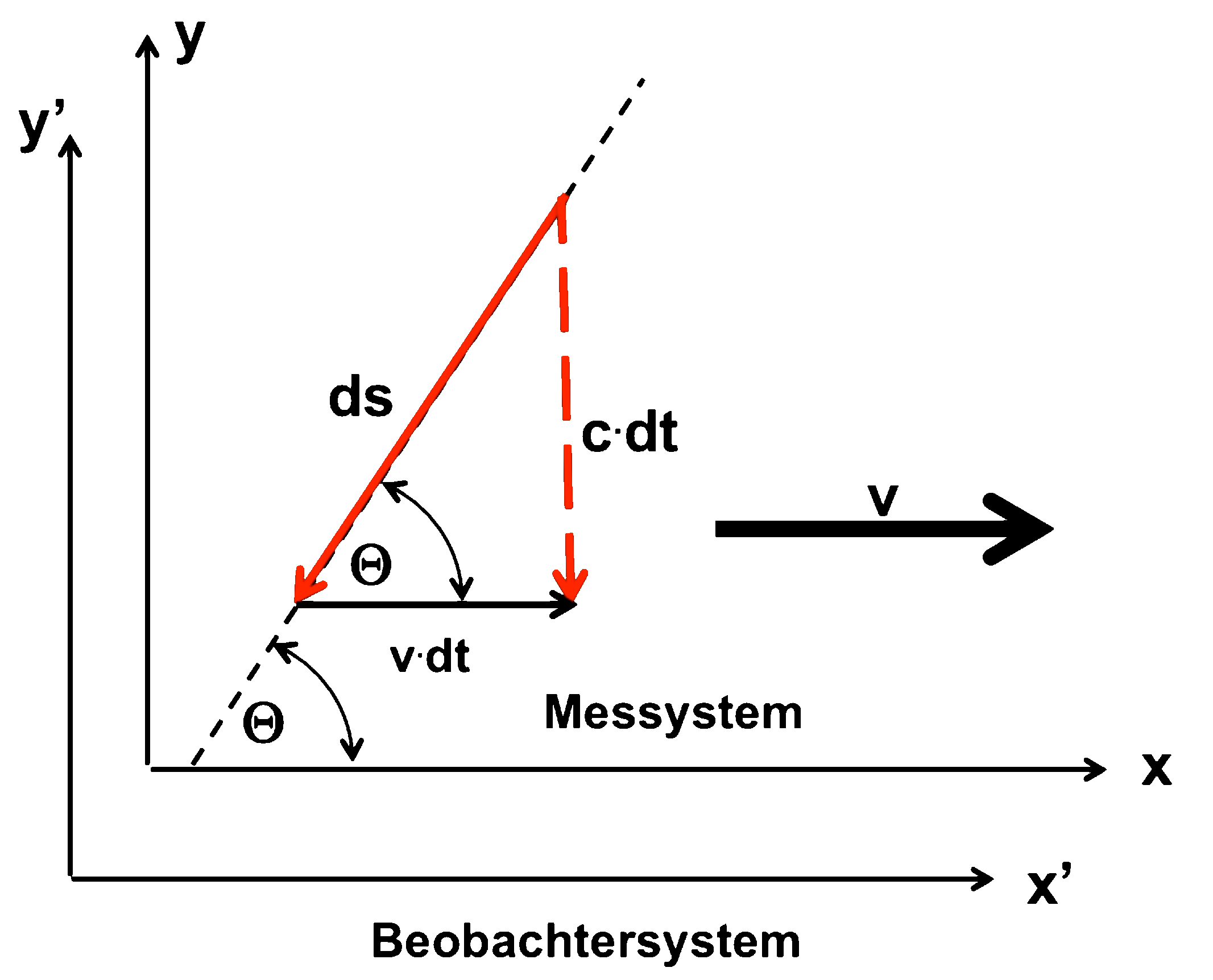
"Way back"
With the above formula it should now be possible to describe the effects observed at the Sagnac and Michelson interferometers without contradiction. At the Sagnac interferometer we are dealing with a rotating system, i.e. there is basically a "resting" observer and a relatively moving light guide system (more details here!)
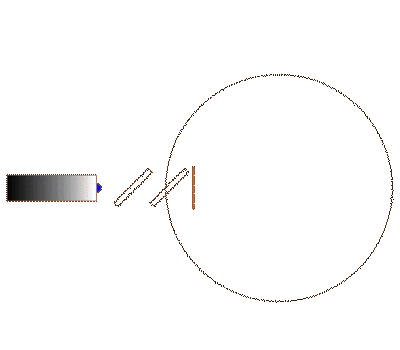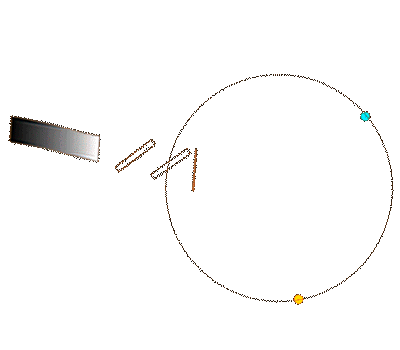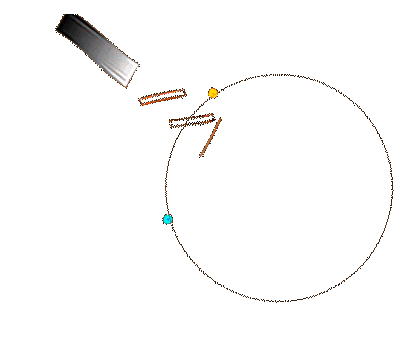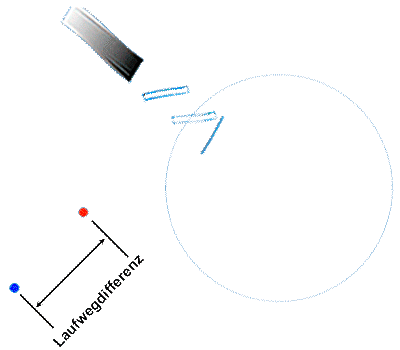
For the imSagnac interferometersFor wave trains rotating in opposite directions, the measuring effect results from the difference in the travel times for the outward and return journeys. (more here.)
dt'sagnac = dt'there - dt'return
Sagnac measuring principle: Runtime difference between the signals circulating in opposite directions.
And because we always want to make life as easy as possible for ourselves, we assume in this case that the structure is circular and that the fulcrum is exactly in the center.
For our question what influence the signal/light speed has on the measuring effect, this is not a limitation of the general validity!
With this simplification ( = 0) we get for the signal running in the direction of rotation:
... and for the signal rotating in the opposite direction:
For the respective signal speeds c'there/back we have to consider that everything takes place in a system that moves relative to the observer and moves with the (tangential) velocity v. I.e. we have to use the relativistic addition theorem forr apply speeds:
where c is the signal speed in the resting system and c0 is the vacuum speed of light as a natural constant!
If one calculates the (Sagnac) runtime difference dt'Sagnac = dt'there - German'return calculated, then you get the somewhat "bulky" expression...
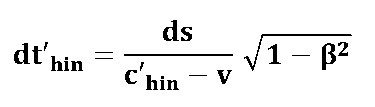
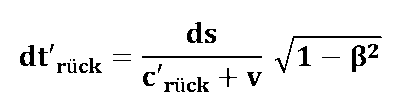
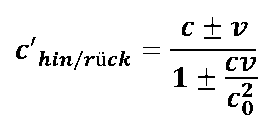
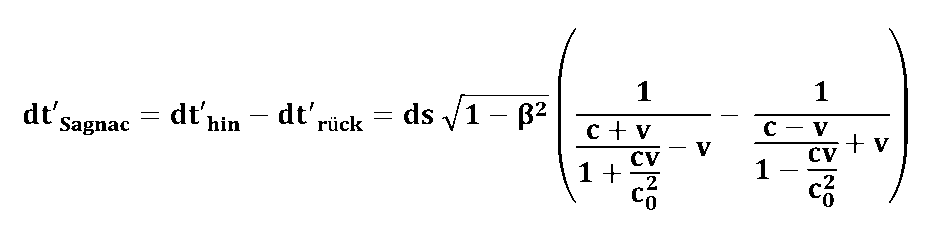
... which, however, after a summary of the many breaks "happily" resolves:
and with. we get the well-known Sagnac formula:
Integrate this expression over a full cycle
and considered. then the Sagnac runtime difference is:
... a relationship that is well known to us!
Take a look at this for comparisonChapter "Sagnac"!
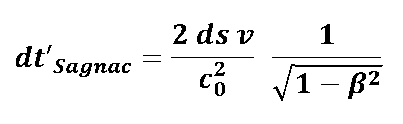
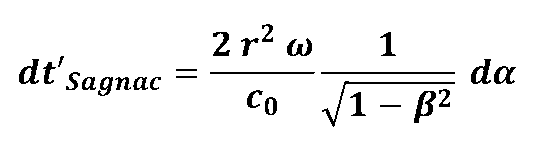
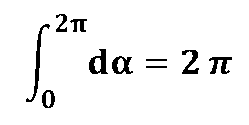
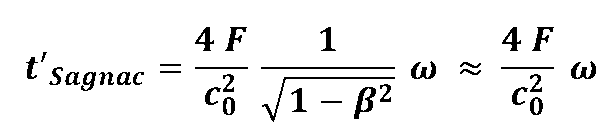

And now ?
What is the point of all the effort when the classical calculation seems to deliver the same result as the relativistic approach?
--> Can I tell you!
In contrast to the classical derivation, we can now clearly see that the formula for the Sagnac transit time difference no longer contains the signal velocity c at all, but only the natural constant c0 (vacuum speed of light)!
This is really a sensation that has two important consequences - one practical and one theoretical:
First the practical:
If the Sagnac effect does not depend on the signal speed, then a very inconvenient source of error is eliminated:
Phase velocity, refractive index and dispersion no longer matter. The only possible error influence is a fluctuation in the interferometer geometry, or the area F, and this should be stabilized quite well by using appropriate temperature-insensitive materials!
And now the "theoretical consequence":
Even if you didn't notice the difference, we now have two formulas for calculating the Sagnac effect that look very similar, but couldn't be more different:
and
The last derived formula for t'Sagnac relativistic no longer the signal velocity c but the vacuum light velocity c0 contains as a natural constant, is of course a result of the fact that we for the signal historywindiness the relativistic addition theorem
have used !


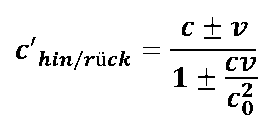
*) A "sound wave ring interferometer" is hardly feasible in practice, - but that shouldn't bother us for the moment!
WR Leeb, G. Schiffner, E. Scheiterer, "Optical fiber gyroscope: Sagnac or Fizeau effect?", Applied optics, Vol 18, No.9 (1979), pp-1292-1295
It is still amazing that the signal speed c no longer appears!
That means that the Sagnac effect also exists for sound waves, for example. *)
The opponents of the theory of relativity - e.g. the Nobel Prize winnerPhilip Lenard - draw the arguments for their criticism of the theory of relativity, among other things, from the fact that the value of the transit time difference in the Sagnanac effect can also be calculated very well using the means of classical physics.
But now it turns out that this correspondence between classical and relativistic physicswas just a coincidence because in all known Sagnac experiments a light wave was used as the signal, the speed of which c was very close to the speed of light in vacuum c0 lay. With the measurement accuracy available at that time, it was not possible to differentiate between them when evaluating the results
With today's technical possibilitiesn it should be possible to decide which approach is the right one - the relativistic or the classical one. This experiment was actually done in 1979 by Leeb, Schiffner and Scheiterer with a glass fiber ring interferometer!
The basic idea of the experiment by Leeb/Schiffner/Scheiterer was to connect the ring-shaped optical fiber path on the one hand and the assembly consisting of the light source and the readout or overlay optics on the other with flexible optical fibers in such a way that this assembly could be moved with the rotating optical fiber and another time resting relative to the rotating fiber optic cable.
In the latter case in particular (readout optics stationary, glass fiber ring rotating) it is to be expected from the point of view of classical / pre-relativistic physics that the light will be carried along in the moving medium. (Fresnel entrainment; see A. Sommerfeld, "Lecture on Theoretical Physics", Vol. IV, p. 58), resulting in a changed speed of light c'there/back leads:
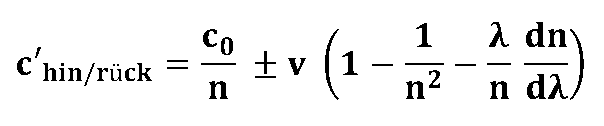
Using this expression for the signal velocity c'there/back is included in the formula for the Sagnac effect and integrated over a full revolution, then the following relationship should result for the transit time difference t'Sagnac:
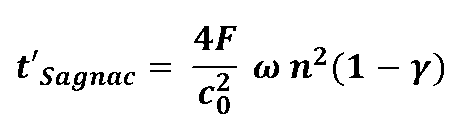

**) Just ask one of the many Einstein critics (e.g.here) how to use this fact without recourse to thetheory of relativity explain!
I admit, - the special theory of relativity (SRT) is a bad impertinence for our imagination and if you "clarity" makes a measure of the correctness of a scientific statement, like the Nobel Prize winner Philip Lenard (Initiator of an "Aryan physics"), then you actually have a problem.
But that doesn't change the fact that SRT is the only one that provides a consistent explanation of all effects related to light propagation in relatively moving systems!
where is the so-called Frensel's entrainment coefficient.
As I said - according to the principles of pre-relativistic physics, the Sagnac effect should depend on the material properties of the light-carrying medium via the entrainment coefficient.
However, in their experiment carried out in 1979, Leeb, Schiffner and Scheiterer were able to show that this is clearly not the case!
It follows:the Sagnac effect is independent of the signal speed **) and that in turn is only understandable against the background of the theory of relativity!
Conclusion: the Sagnac effect is thus purely a relativistic effect !

There are few examples where relativistic effects are so become macroscopically visible!