spez. Relativität

The special theory of relativity - as far as they for the descriptionng of the Sagnac effect is required !

Yes, I know: Introductions to the special theory of relativity are "a dime a dozen".

Either the authors try to curry favor with the reader, according to the motto: "Look here, I'm the great explainer of the world - it's all very simple", or they wrap themselves in the fog of a great theories in the sense of "Except for me, no one understands that anyway! "

I probably belong to the first category, I love simple explanations even at the risk of (sometimes) inadmissible simplifications creeping in with them.

We have gotten used to the fact that relativistic effects (time dilation and length contraction) play practically no role in everyday life because they are far too small. The optical "Gyro" is one of the few devices - maybe also the GPS Navigation ! -, in which relativistic effects lead to a concrete "tangible" result that can be observed with the "naked eye"!

"explain" is the wrong word here!

According to Wikipedia, EXPLANATION means naming the causes of a phenomenon; an EXPLANATION is convincing, makes sense or is satisfactory.

The statement that the speed of light is a constant in all frames of reference just doesn't do all that!

But it is not important whether this statement makes sense to us or whether it convinces us - what is important is: can the observations in nature be described with this statement or not.

So come on, - how do we want to approach the matter?

We should first look at the twobasic postulatesof the theory of relativity and then examine whether the experimental results are satisfactoryexplained can become:

postulate 1. The same laws of nature apply throughout to all systems moving uniformly against one another.

postulate 2. The speed of light is a constant in every frame of reference.

Postulate 1 is the one already recognized by Galileo and Netwonprinciple of relativityp, - here, however, in the formulation ofA Einstein.

Postulate 2 is the result of a centuries-long search for the nature of light or electromagnetic waves.

Thousands of experiments on the nature of light before and after Einstein can only be explained by the observation that light travels always and everywhere at the same speed; Einstein therefore extended Galileo's principle of relativity to include this point.

So what does that mean in practice -

first to postulate 1 - Galileo's principle of relativity:

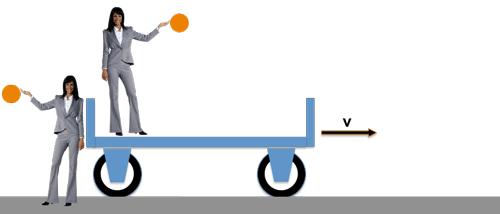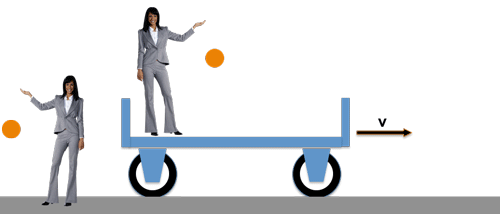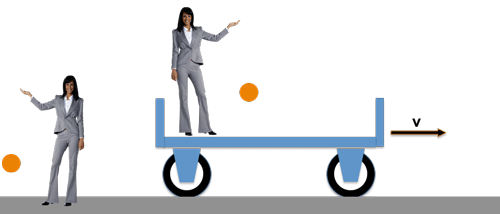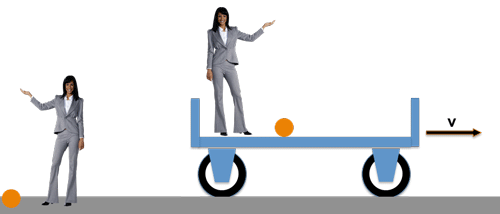
Incidentally, this also applies to experiments in the field of electrodynamics, optics, thermodynamics, etc., because that is precisely what Galilei’s principle of relativity says:
>> The same natural laws <<

The lady on the carriage moves with the same speed v compared to the other lady on the platform. Both carry out a fall experiment and both observe exactly the same thing: the ball falls straight down from the same height in the same time - because the same law of falling applies to both!

The lady on the carriage will not be able to see any effect of the carriage speed v on the movement of the ball in her "reference system" .....

..... and the lady on the platform has no reason to doubt the validity of her observation anyway, although her "reference system", namely the platform, is actually traveling quite fast together with the earth!

As far as the classic relativity principle postulate 1.

This comparison of the different propagation speeds, e.g. of light, water, sound waves or even projectiles and water jets is very problematic and basically even wrong:

--> comparing apples to pears here:

The velocity of a cannonball, or a jet of water, is of course also affected by the velocity of the "source"; the muzzle velocity and any movement of the gun, of course, add up to an overall velocity.

It is completely different with a sound wave: its propagation speed depends only on the properties of the carrier medium and is completely independent of the speed of the source - as can be observed very well in supersonic aircraft. Here the source (the plane) "overtakes" even its own wave!

FA-18_Hornet_breaking_sound_barrier_(7_July_1999)_-_filtered.jpg

Nevertheless, the additivity of the speeds also applies to sound propagation, we only have to clearly distinguish who or what is moving in relation to whom. In the case of sound propagation, it is about the relative movement between the carrier medium and the observer!

What remains to be noted:

In terms of its speed of propagation, light does not "behave" like a projectile, and a carrier medium as in the case of sound has never been demonstrated.

Some experiments indicate that light is a transverse wave (polarization), others can only be explained by a particle idea (photo effect).

So what is light? Since Einstein, (most!) physicists have stopped trying to answer this question; we take note of the various effects and manifestations - and that's it!

postulate 2.The speed of light is a constant in every frame of reference.

Now we come to the second part of the "special" principle of relativity:

The speed of light is a constant in every frame of reference.

What does that mean concrete ?

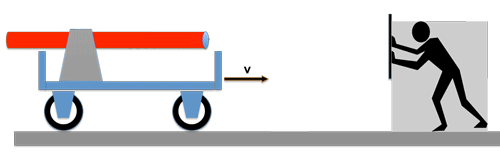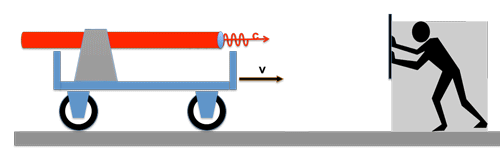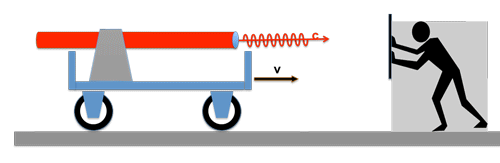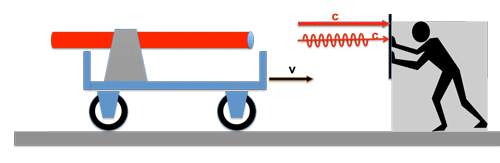
Let's imagine the following experimental setup:

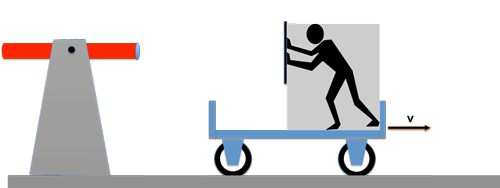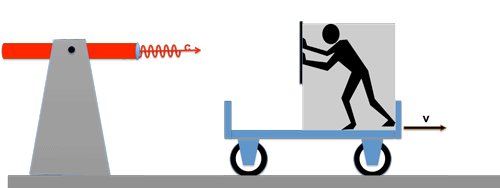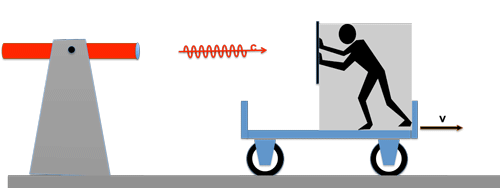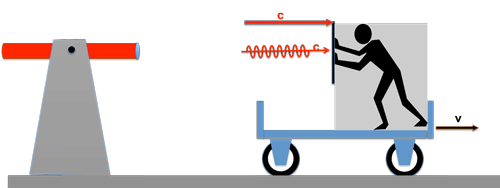
A light wave train is sent from a stationary light source with the speed c behind a moving car; the car has the speed v.

There is an observer on the carriage who has the task of measuring the speed of the incoming light beam. How he does it shouldn't bother us at the moment! What do you think the result of its measurement will be? --> Correct: the speed of light is still c!

No matter how fast the car is going, to the observer on the car, the speed of light is always the same!

Let's turn the situation around:

Now we mount the light source on a carriage and let it drive towards the observer with the velocity v. Even now nothing will change for the observer: he will still measure the same speed c of the light wave train as before!

Imagine if we had carried out the above experiments with a water syringe instead of a light source. The speed of the water jet is w.

The result of the speed measurements for the water jet would have been quite different; the speed v of the car would have been clearly noticeable: --> In the first case, the jet of water would have hit the carriage with a velocity (w-v), in the second case, the resting experimenter would be hit by a jet of water with velocity (w+v).

The statement "the speed of light is a constant in every frame of reference"

means:

--> the conventional addition of speeds does not apply to light!

Regardless of whether the transmitter and / or receiver move in relation to each other or not, or whether the receiver moves in relation to a (hypothetical) carrier medium the "ether" or not, the (vacuum) speed of light always remains the same!

And please do not confuse -

the speed remains constant - but not the frequency!

The statement that the speed of light is constant in any frame is consistent with "common sense" and/or the "opinion" hard to believe, but you will see that all experimental findings can actually be explained with this assumption. (So far we haven't come up with anything smarter!)

Here again the two Postulates of the theory of relativity:

1. In all systems moving uniformly against each other, thesame laws of nature.

and

2. The speed of light is a constant in every frame of reference.

Before we consider how the two principles"marry" each other, we have to go one step further:

So far, we have only concerned ourselves with how the situation is presented within the respective system. We have found that the same physical laws apply and we have come to terms with the fact that a light wave train always has the same speed - no matter where the source is or at what speed it is moving relative to the respective frame of reference; we don't like it and it causes spasms in the world of our everyday experience, but that's the experimental reality!

Basically, everything is very simple as long as we do not leave our reference system - e.g. the railway carriage rolling along steadily:

--> The well-known laws of nature always apply and when we encounter a ray of light, it always has the same speed, no matter whether it comes from a moving or a still source is sent out!

So far so easy!

In the special theory of rativity, however, there is a somewhat more far-reaching question - namely the question of how a physical law, e.g move speed. (Hence the name "relativity" theory!)

That sounds a bit theoretical. To clarify, let's go back to our first "falling balls" example:

You remember: the laws of falling are exactly the same in a reference system at rest as in a system in constant motion (railway car or ship); so far so clear!

However, you will not recognize the law of falling if we ask the experimenter to observe the experiment from "outside", from a "resting" position, e.g. with binoculars. Now the path of the falling ball could look something like this:

Please excuse the somewhat awkward animation!

This is not new and has been known since Galileo.

Attention: this is the crucial statement!

To the observer outside the car, the ball does not fall in a straight line; it moves with the carriage and goes through something like a parabola of throwing. The observer outside the car could deduce the speed of the car v from the trajectory of the ball. This is not possible for the observer in the car, for him the ball still falls vertically!

So it makes a big difference whether we observe an experiment "inside" a uniformly moving frame of reference, or from "outside", i.e. from a second frame at rest relative to the first.

And now comes the crucial new step:

Let's now bring the constant speed of light thing into play, i.e. let's look at situations where light matters!

If the speed of light is always the same, i.e. if the light "evades" the "normal" law of addition for speeds, then one must expect that the lengths and measurement of time within the relatively moving system will also change, in the sense that the law of addition for the (vacuum) speed of light no longer applies and a kind of transitional solution exists for the addition of very high speeds.

That sounds very cryptic and: YES, you are right: that is also difficult to imagine!

Let's take a look at the timing first!

The time dilation.

There is, for example, the famous "Light Clock":
The basic idea is actually brilliant!

If the speed of light is always and everywhere constant, then one could make excellent use of this to construct an extremely stable running clock!

To do this, we let a light pulse run back and forth between two mirrors and every time the light pulse arrives at its starting point again, a counter jumps one step further.

At a speed c of the light and the distance LE between the mirrors, the running time is

tE = LE / c

Next, we mount this "light clock" on a carriage traveling at speed v.

Nothing changes for the accompanying observer:

The "Light Clock"

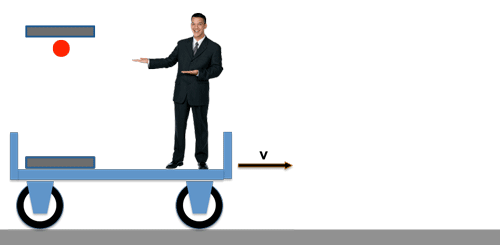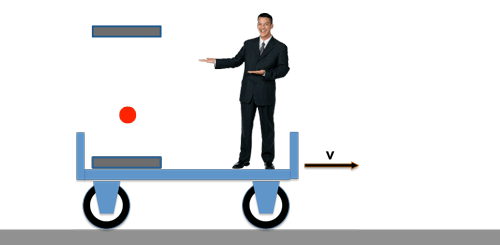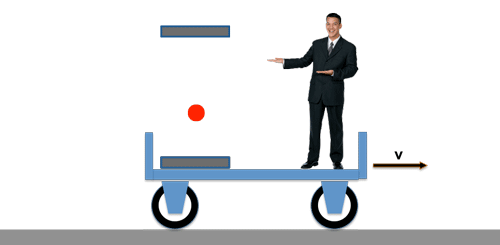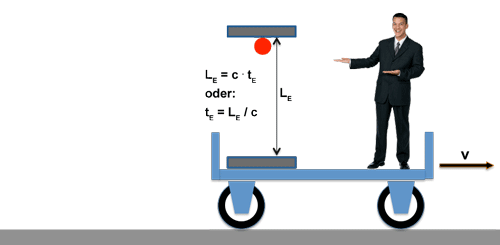
The running time of the light between the mirrors - and thus the clock frequency of our "light clock" - is still:

tE = LE / c

In the next step we leave the observer at the side of the road, but everything else stays as it was. For the observer at rest, however, the experiment now takes a completely different course:

As I said: - we haven't changed anything at all on the "Lichtuhr". Only the position of the observer is different and just like in our case experiment above, the light wave train now takes a completely different path. Since the speed of light is constant, in contrast to the speed of the falling ball, the light travels on a straight zigzag path and not on a curved throw parabola - but that need not concern us for the moment.

Much more exciting is the following Ask:

Does our "light clock" work the same way for the stationary observer as it does for the one traveling with us? Has the clock frequency changed?

To do that, we need to take a closer look at the situation and those of the lightLE and from the wagonLW analyze distances covered:

LE = c . tE is the path of the light wave from the point of view of the traveling observer;
LR = c . tR is the path of the light wave as seen by the observer at rest;
LW = v . tR is the path of the car as seen by the observer at rest;

We don't really need to do any further calculations at this point:

You can see very easily that the path of the light wave from the point of view of the resting observer LR is longer than the path from the point of view of the traveling observer LE and if the path is longer, the light wave takes more time, in short:for the resting observer the light clock runs slower!

But in order to find the connection to the standard literature, we can also use this insight with somethingtrivial mathematics garnish:

The whole is a right triangle and we can apply the Pythagorean theorem:

and the above relations for the walking distances LE, LW and LR insert:

after the observer's proper time tE resolved results in:

...by simply rearranging the equation....

Or in sthas the more well-known notation:

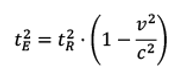
What just happened here?

We've changed locations and the clocks are already slowing down!

How come ?

At what point did this effect appear in our calculation?
We only have a very simple triangular calculation for the walking distances LE, LR and LW carried out!

Again - where is the "sticking point"?

The answer is as simple as our whole calculation:
We havethe signal or light speed c kept constant, - is that actually correct? From the point of view of normal everyday mechanics, not really!

Just think about it:

- from the point of view of the moving observer on the car, the speed of the light pulse between the mirrors is c - that's clear!

- from the point of view of the observer at rest, we have also set c for the speed of the light pulse, true to the principle of relativity "The speed of light is a constant in every frame of reference".

But according to our "everyday experience" we should have also considered the speed v of the car from the point of view of the stationary observer for the signal speed! If we do that, all the spook will be gone!

So the thing about the clocks going slower follows very directly from the postulate:

>> the speed of light is a constant <<

In the following section we carry out the whole calculation again, but this time we also take into account the car speed v in the signal speed and you will see that nothing remains of the time dilation.

You can also simply skip the following section - it only shows that our everyday mechanics fail in deriving the experimentally proven (!) time dilation.

"Time dilation" - from a classical point of view

From the speed of light c and the speed of the carriage v, the resulting speed c' results (from the point of view of the stationary observer!). (so.)
You can calculate very easily with the help of the Pythagoras relation:

the relationships for itineraries LE, LR and LW are as follows:

The theorem of the Pythagoras:

However, for LR we have to consider that we now have to use the signal velocity c':

With the above relation results from this:

or: tE =tR

or in words: Proper time in the reference system = time of rest system

i.e. if you put the assumes classical additivity of velocities, then the time in the rest system is identical to the time in the relatively moving system (frame of reference).

The two clocks are the same - the time dilation effect has disappeared!

c : Signal / Light Speed

v : carriage speed

c' : Signal speed from the view

of the observer at rest

LE : path in the moving system

LW : (walking) route Of the car

LR : Path from the point of view of

rest system

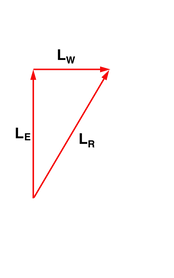
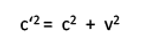
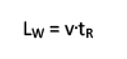
tE : Proper time in the moving reference system
tR : Time from the point of view of the rest system

critical note !

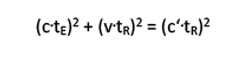
'sorry, the example isn't very original; I couldn't think of anything better!

The length contraction

The fact that we basically have to assume the speed of light to be constant everywhere forces us to redefine other elements of our everyday mechanics - e.g. the length of a moving body or the length of a distance ... and we have to be very precise here too distinguish from where we observe the process.

Let's look at an example:

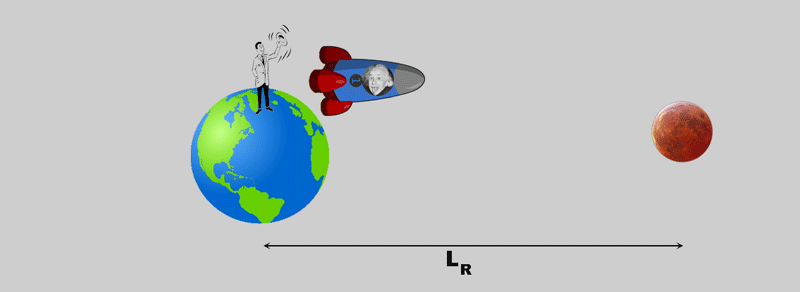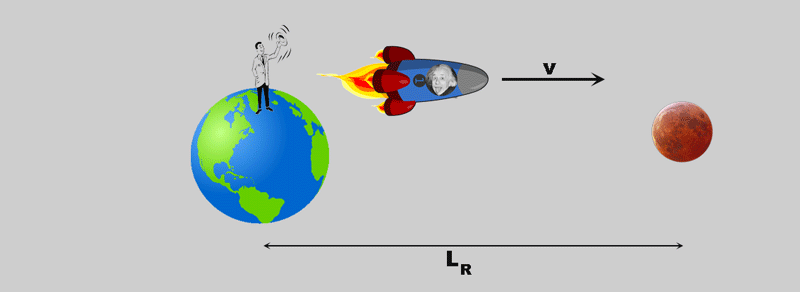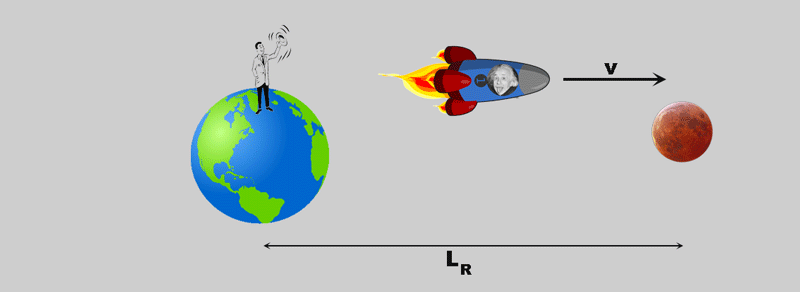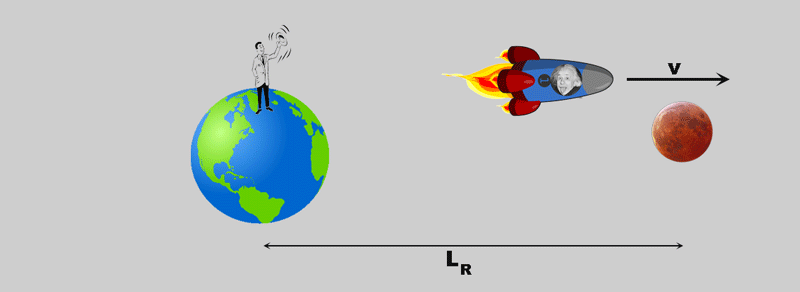
A rocket starts from the earth, let's say: to the moon.

For theObservers on Earth - the "rest system" - does it look like this:

- LR is the distance traveled by the rocket;
- tR is the time that elapses
- v is the speed of the rocket.

Theobserver in the rocket has a slightly different impression of what is happening:

- the "rest system" (Earth-Moon) moves under it;
- from his point of view, he covers distance LE;
- the time that elapses is tE;

However, the two observers on earth and in the rocket agree on the speed at which they move against each other - it is v !

What was our goal ..... ?

... as a reminder:

We are in the process of investigating whether stretches (in our example LR and LE) each from the point of view of the resting or of the moving observer and if so, by how much.

We already have all the information together - we just have to organize it. Let's go:

The velocity of the rocket as seen by the observer at rest is:

v = LR / tR

The velocity of the rocket as seen by the moving observer is:

v = LE / tE

Since the velocity v must be the same for both observers, the following applies:

LE / tE = LR / tR

or:

LE = LR . (tE/tR)

The connection between the proper time tE in the moving system (the rocket!) and the time tR in the rest system (on earth!) we already know (so.):

with

If we convert this expression into the above relation for LE insert, then we get:

or:

i.e. from the point of view of the moving observer, distance LR (between earth and moon) is increased by the factor shortened - this is the so-called length contraction !

In our day-to-day mechanics, however, this doesn't matter too much; an example:

Let's take a car that drives at 100 km/h. For the observer on the side of the road, the clock in the car is therefore increased by the factor: 0.999 999 999 999 995 run slower than his own; i.e. after approx.3.5 million years the two clocks show a difference of 1 second !

However, if the "car" is traveling at half the speed of light (150,000 km/s), then the correction factor is 0.866.

Now the two clocks already show a rate difference of 1 second after 7 seconds!

But cars that are 150,000 km/sec don't exist yet ;-) ... and even the fastest rocket (Helios 1 and 2) with approx. 70 km/sec is no competition for light!

So, we now have the first and probably also the most well-known elements of the special theory of relativity together:

- thetime dilation - moving clocks go slower!

and

- thelength contraction - the distances in relatively moving systems are shortened

... and again as a reminder:
We had to introduce these corrections in the measurement of length and time in order to fulfill the condition that the speed of light c is fundamentally constant everywhere, in all systems moving against each other!

I don't think that was too difficult so far - we only have to think through the thought of a constant speed of light in all reference systems and we end up with time dilatation and length contraction!

But unfortunately - the whole thing was just a "finger exercise" so far, because if we want to understand the Michelson and Sagnac experiments correctly, then we have to go one step further:

--> we need to understand how the velocity of a signal is calculated when it is composed of two partial velocities.

Here is the (somewhat clumsy) example: A small wagon on top of a large wagon.

- A carrier wagon moves with the speed v

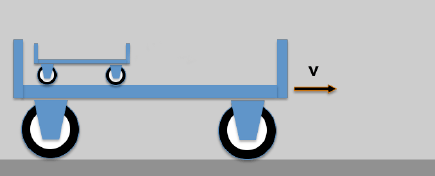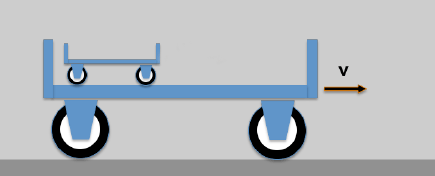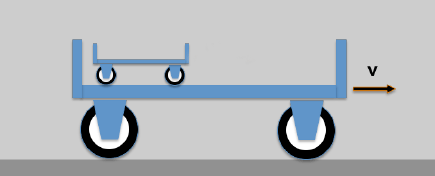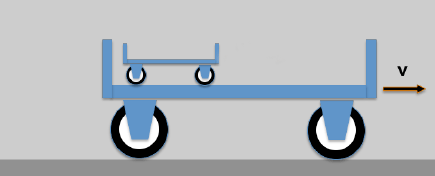
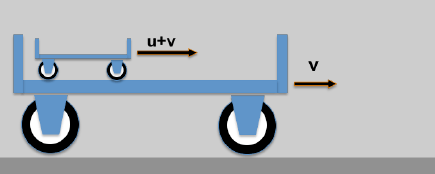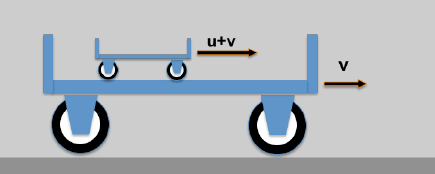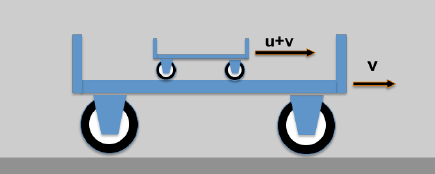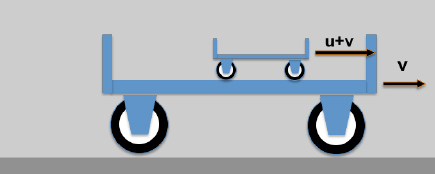
- On the carrier wagon there is another wagon that is moving (opposite the carrier wagon) with the speed u; a resting observer will then see the following:

*) 10-4c is 30 km/sec; this corresponds to the speed of the earth in its orbit around the sun!

We are always talking about the vacuum speed of light c!

Requirements for an addition theorem for velocities:

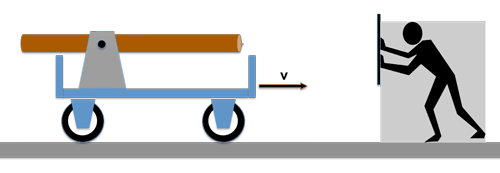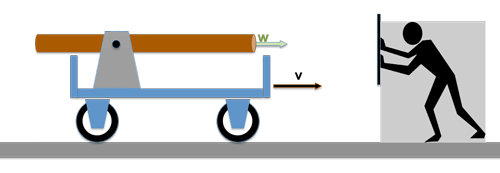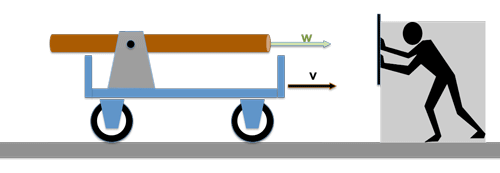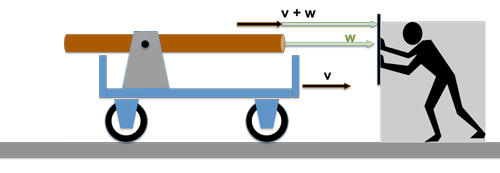
The resulting speed of the little car would be an observer (who has never heard of the theory of relativity) with w = u + v indicate.

"Well," .... you will say, "why is he telling us that? That's trivial!"

I have to disappoint you: the "addition" of velocities that we have just practiced is unfortunately not at all trivial and for very large velocities - close to the speed of light c - the above expression ( w= u + v ) is actually wrong!

Let's take another example:

The speed of the carrier system (this can be an optical device, for example).
10-4c*); a light wave train runs in this device with the speed c .

For an observer at rest, the resulting velocity would then be according to the classical addition method

1.00001.c

amount to, - i.e. lie above the speed of light c, which cannot be - because the speed of light is a limit speed and

.... the speed of light is a constant in every frame of reference!

(see above - 2nd postulate!)

So we need to find an addition theorem for velocities that has the following properties:

1. The resulting speed must never be greater than the speed of light c;

2. For small velocities (approximately) the classical addition theorem should
( w = u+v ) apply.

All right: Michelson ultimately did not want to determine the speed of his interferometer, but rather to prove the existence of a carrier medium for light waves, the so-called ether, but for this he also had to know the signal speed.

Why is this so important for the Sagnac interferometer?

The device is intended to measure the propagation time of (light) signals in a (carrier) system that in turn moves or rotates at a certain speed. The aim of the experiments is to use the transit time of the light signal to deduce the movement or speed of the carrier system!

In order not to make a mistake here, we have to examine very carefully how the velocity of the carrier system (=interferometer) and the signal velocity are composed for the stationary observer (!).

By now you know these little sketches well enough - what do you see?

- a stationary observer stands next to a carrier system that moves with the velocity v relative to its position;
- on the carrier system there is a source which emits a signal with the speed c relative to the carrier system;
- the observer knows the signal speed c and would like to determine the speed v of the carrier system from the propagation time of the signal over a certain distance;
- he must answer the question at what speed the signal spreads from his point of view.

In classical physics he would have added the speed of the carrier system v and the signal speed c, - but we know that from the point of view of the 2nd postulate (the speed of light is a constant in every reference system!) is wrong.

Don't worry - we already have so much basic knowledge that we can still reach our goal quite quickly! So it doesn't help, we have to deal with the question of how velocities are to be added against the background of the two relativistic postulates and as usual, we start - once again - from the beginning!

Galileitan formation

What does the theory of relativity deal with?

In short - it's about reference systems that move relatively against each other - hence the name! - and the influence of this movement on physical quantities.

We have already established that we have to correct the measurement of time and the measurement of length if the reference frame in question is moving at a constant speed.

We now want to ask ourselves the question of how to convert the coordinates of the stationary reference system into those of the moving one and we will start with the classic approach:

The Galileo Transformation

... and because we want to make life as easy as possible for ourselves, the coordinate axes of the two reference systems are parallel to each other and the direction of movement runs exactly in the direction of the x-axis, something like this

Example:

If the moving reference system (x', y', z') moves with the speed v in the direction of the x-axis, then it lays the path v in the time t'.t' back - namely in the x-direction. I.e. the relationship between the x and x' coordinates can be easily represented as follows:

x = x' + v.t'

By exchanging the coordinates x and x', or t and t', the position of the observer can also be shifted from the unprimed to the primed reference system; however, the sign of the velocity v has to be changed - I think that's pretty clear.

x' = x - v.t

(Formally, we simply solve the above equation for x'!)

For the other coordinates everything stays the same:

y = y'
z = z'

and of course nothing changes in time either:

t = t'

However, from our consideration of length and time measurement in moving systems (see above), we know that moving clocks run differently - namely more slowly - and that the distances in the direction of movement are shortened!

However, these effects are not covered by the Galilean transformation.

That means we have to take care of a more general transformation!

But first we should consider which properties this new transformation must have:

1. The transformation must be linear, i.e. the transformation must map straight, uniform movements back to straight, uniform movements.

2. The new transformation must apply to all points in time and space.

3. For small relative velocities between the reference systems ( v << c ) the new transformation must change to the Galilean transformation (see above);
4. The new transformation must be independent of the direction of movement (+v or -v).
5. The new transformation must be symmetrical with respect to the reference systems, i.e. it must not matter which reference system is taken as the reference.
6. The new transformation must include the speed of light as the limit speed.

These are the properties ofLorentz transformation

We should now set about deriving them.

Equation 1a / 1b

Equation 2a / 2b

Equation 3a / 3b

Equation 4

Equation 5a

Equation 5b

The Lorentz transformation

Exactly as above with the Galilean transformation, we reduce our considerations to the special case that the movement of the two reference systems runs parallel to the x or x' axis.

You have to admit that the properties of the transformation formulated above are obvious and actually self-evident!

We now approach the problem very mathematically.

We assume that the Galilean transformations:

x = x' + vt' or x' = x - vt

must be supplemented by the factor k so that they meet the above conditions 1. - 6., i.e.:

x = k.(x' + v.t') and x' = k.(x - v.t)

and this factor "k" has to be determined.

If we apply the above conditions to the factor "k", then:

- from 1 follows --> k must not depend on the spatial or time coordinates;
- from 3 follows --> for v --> 0 follows k --> 1
- from 4+5 follows --> k(-v) = k(+v)
- from 4 follows --> k(-v) = k(+v), this could mean k is a function of
- --> k must be dimensionless, i.e. k is a function of

In addition to the transformation of the spatial coordinates (x,y,z) and (x',y',z') follows from the 2nd postulate ("the speed of light is a constant in every reference system) that we also need a transformation between the times t and t'. Since a light signal moves independently of the position of the observer with the speed c spreads, the following applies:

v = c.t and x' = c.t'

What follows is a rather tiresome but ultimately trivial shuffling of the above equations; I don't want to deprive you of this acrobatics of equations - but you can safely skip them!

To determine the Lorentz factor k, we first need the coordinate transformations:

x = k.(x' + v.t') x' = k.(x - v.t)

and

x = c.t x' = c.t'

by inserting 2a / 2b into 1a / 1b we get:

c.t = k.(c.t' + v.t') c.t' = k.(c.t - v.t)

Multiplying Equations 2a and 2b:

Now you solve the whole thing for the Lorentz factor k and get:

What we are still missing are the transformation equations for time:

with c.t = k.(c.t' + v.t') converted to t= k.(t' + v.t'/c) and x' = c.t' converted to t'=x'/v we get :

and by analogy:

Let's do the equations ofLorentz transformation summarize:

   x = k.(x' + v.t')       x' = k.(x - v.t)
y = y'    y' = y
z = z'    z' = z
   t = k.(t' + v.x'/c2)       t' = k.(t + v.x/c2)

with: and:

You can check whether the above-mentioned properties of the Lorentz transformation are really maintained, e.g.:

3. For small relative velocities between the reference systems ( v << c ), the new transformation must change to the Galilean transformation.

Let's assume that the relative speed is v =0. From this it follows that k = 1 and for the coordinate transformations we get:

x = x' + v.t'
y = y'
z = z'
t = t'

... so the normal Galileo transformation! (s.d. here)

May I remind you why we bothered with the Lorentz transformation in the first place?

--> We wanted thoserelativistic addition of velocities derive

So again:

- You are standing next to a car which - relative to you - is driving with the speed v.
- a second carriage drives on the carriage with the speed u, - relative to the first Dare
- what is the speed w of the second car relative to your position?

In general, the speed w is described by

w = x / t

We now have to transform x and t into the coordinate system x' and t' using the Lorentz transformation and insert it into the expression w = x / t:

This is a bit "confusing" now, but we're going to simplify it in a moment!

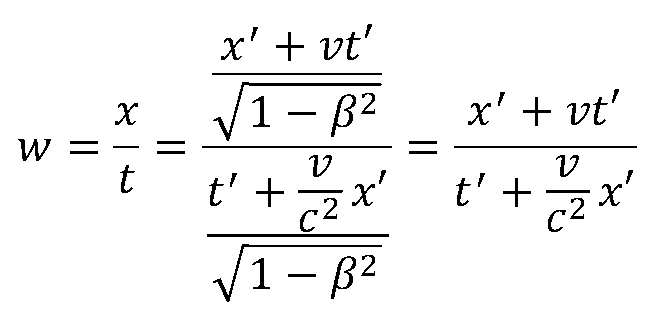
In the next step we divide the numerator and denominator by t' and get:

relativistic addition of two velocities:

x' / t' describes the speed u in the moving (x',y',z',t') system, i.e.

That follows from that

relativistic addition theorem:

.. and with that we have the relationship that describes the addition of two velocities u and v according to the principles of the special theory of relativity!

So, now we have the tools together that we need to be able to describe the effects observed at the Michelson and Sagnac interferometer correctly, but above all without contradiction:

The Michelson interferometer can already because of the classical principle of relativity according to Galileo Gililei show no walking path effect, but the relativistic description shows that the observer at rest can't register an effect.

The Sagnac interferometer does react to rotational movements, but the relativistically correct description makes it clear that this effect is completely independent of the signal speed. This special property of the Sagnac interferometer qualifies the device as a precision sensor, but also makes it clear that the classic - non-relative description must be wrong, because the formula for calculating the travel distance difference contains the speed of light c, but not as a parameter of the light source used, but as a natural constant. (as a natural constant, "c" enters the description of the output signal via the realistic addition theorem - the signal speed itself is omitted!, s.d.Sagnac II .)