Michelson | Sagnac

The Michelson experiment - a failure with great impact

.... or: how to measure 10 exp-16 sec ? (click here)

Albert Abraham Michelson
19.12. 1852 (Strelno, province of Posen) - 9.5. 1931 (Pasadena California)
1907 Nobel Prize in Physics
Measurements of the speed of light and proof of the ether as the carrier medium of the light waves.
(more)

At the end of the 19th century, physicists were concerned with the nature of light; In particular, it was about the question of whether - similar to the sound wave - there is a carrier medium for light or for electromagnetic waves exist.

man called this medium ether. (Some from the physical lateral thinker scene are still looking for it today!)

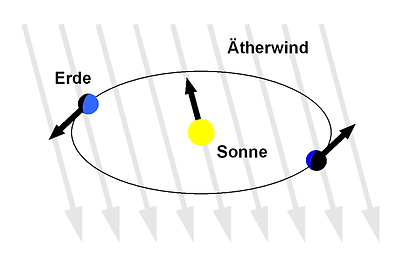
A widespread notion among physicists of the 19th and early 20th century was that this "ether" fills the entire universe and that the earth is moving through this "sea of ether" at a speed of about 30 km/s on its way moved around the sun. (If you take into account the movement of our galaxy, then it is even moving at 200km/s!)

I.e. the earth would have to be subjected to a considerable "ether wind" (probably better "etherstorm") that either slows down or transports a light wave - depending on the direction of travel.

The basic idea was that a light wave once to run in (ether) wind direction and once perpendicular to it and to determine the running time. If the light in the ether behaves like the sound in the air, then there should be a difference for the two directions of propagation!

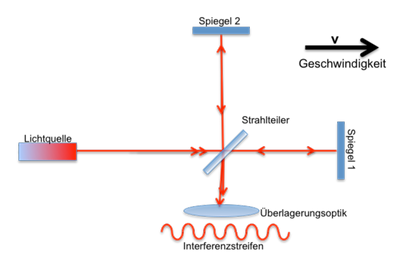
Michelson used the following experimental setup:

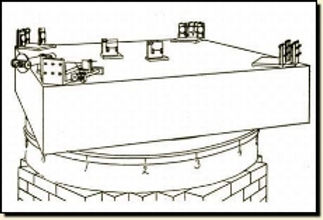
Since this is one of the most important experiments in the history of physics, I don't want to withhold the original picture from you:

Image: source

The following basic sketch is a bit clearer and therefore perhaps easier to understand:

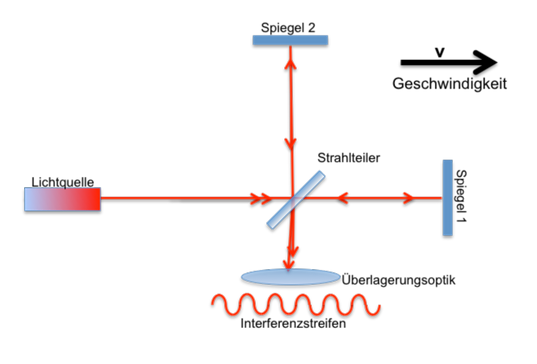
You don't need to understand the "interference fringe pattern" thing here; see further for a detailed explanation below!

A light wave train emanating from the light source is divided at the beam splitter (semi-transparent mirror). The device is aligned in such a way that the optical path between the beam splitter and mirror 1 runs parallel to the direction of movement of the earth and the path to mirror 2 runs perpendicular to it.

After a certain running distance - with Michelson it was 11m (!) - the light wave trains are reflected at mirrors 1 and 2, run back to the beam splitter, are superimposed there and form an interference fringe pattern.

That is, according to Michelson's idea, the light wave train is exposed to a considerable counter (ether) wind on the way to mirror 1, on the way back to a corresponding back (ether) wind and he hoped to be able to prove the effects of this ether wind with this experimental setup

At rest, things look something like this:

The Michelson interferometer:

A light beam travels from a light source to a beam splitter; there it is split. The two partial beams run perpendicular to each other to a mirror, where they are reflected and then superimposed again at the beam splitter.

Depending on the path length in the two sections, the light waves meet at the beam splitter with a certain phase position - in the example we have assumed that the light wave trains arrive at the beam splitter in phase and leave the beam splitter again in phase.

To make it clear that the signal is a light wave with a fixed wavelength, I have used a piece of "pearl necklace" was selected. The smaller the beads, i.e. the shorter the wavelength of the light used, the more precisely a relative change in the path between the two paths can be detected.

So now let's set the whole machine in motion:

The distance traveled in the two arms of Michelson's interferometer was 11m, i.e. 22m there and back. With a speed of the earth of 30 km/sec, a light speed of 300,000 km/sec and a light wavelength of 0.45 microns he expected a phase shift of about 0.4 interference fringes (= beads).

You can find the exact calculation for thisbelow!

Michelson-Chain-in-Movement-V3-with-frames-550x300pt-new.gif

Configuration I is the arrangement that Michelson had in mind: the experimenter or the observer moves through the "ether" with the device

Configuration II should also be considered for the sake of completeness - but I am not aware of an experiment of this type.

.... and as you can see, we can expect a small travel path shift between the two light wave trains at the exit of the interferometer!

Speaking with Michelson of the existence of an "ether" as a carrier of light waves, we basically have to assume two different configurations:

--> I In the first case the observer moves with the device;

--> II. In the second case the observer is outside the device - he "rests" in the ether and the device moves relative to the observer.

In both cases the device (interferometer) moves with the speed v through the ether.

Configuration I: Moving Observer:

1. The Michelson experiment moves with velocity v;

2. the observer is moved;

3. There is an ether wind in the device

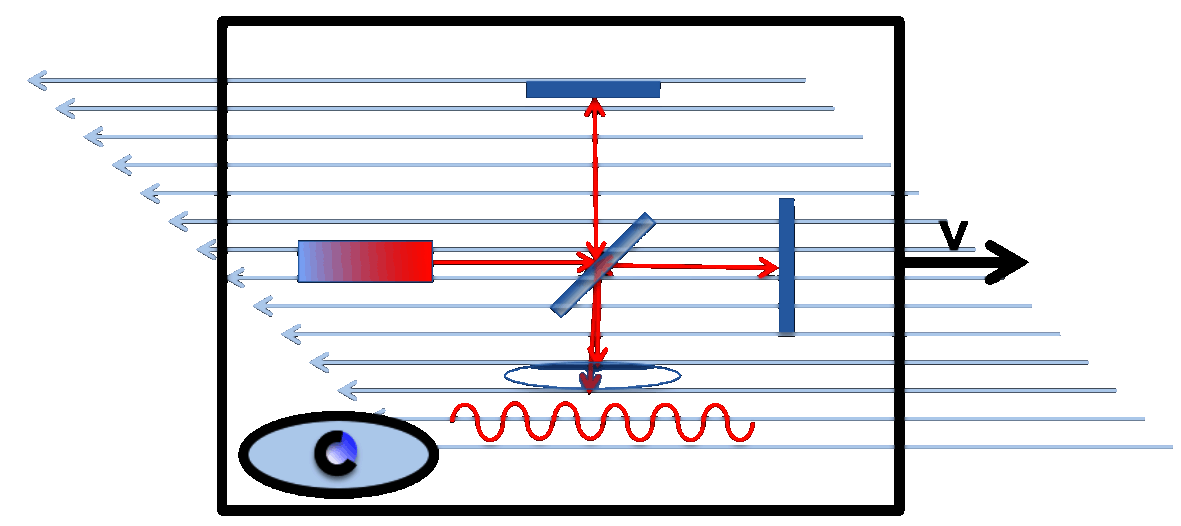
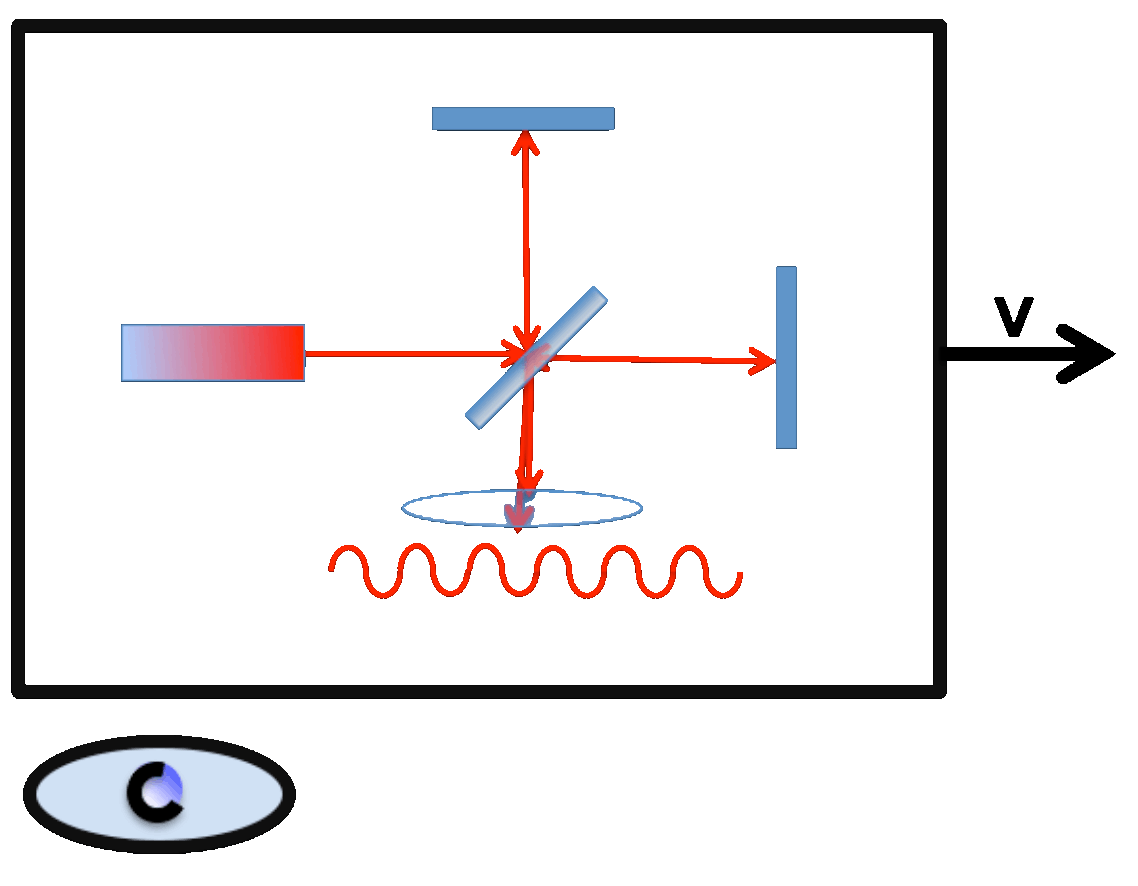
Configuration II: Resting Observer

According to the principles of classical / pre-relativistic physics, it should also be possible for an observer who is at rest with respect to the measuring system to detect a walking path effect; this does not even require the hypothesis of an ether wind!

1. The Michelson Experimentmoves with speed v;

2. the observer rests outside the experiment.

3. There is no ether wind in the device

Configuration I

- the interferometer is traversed by an aether wind, the observer is also moved: (This is the configuration that Michelson actually had in mind when he was experimenting!)

In this configuration, the entire experimental setup, the interferometer and the light source, stationary relative to the observer; only the sought-after "ether" is in motion. According to Michelson's idea, the light wave train must prevail against an ether wind on the way between the beam splitter and mirror 1, so that its resulting speed is reduced; it is c-v . The running time for the outward journey is therefore extended. Or as a formula (L: path length; c: speed of light; v: speed of the device compared to the ether)

On the way back from mirror 1 to the beam splitter, the speed of the light wave train is increased to c+v by the (back) aether wind, i.e. the transit time dt- for the way back is:

The total running time between the beam splitter, mirror 1 and back now results from the sum of dt+ and dt- :

or after some transformations: with:

Please make a note of this result - we want to look at the other possible configurations first.

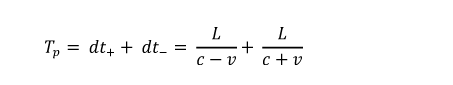
Configuration II

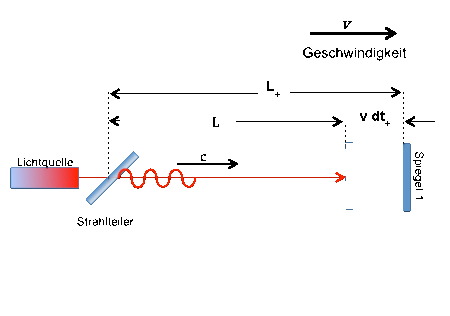
- in this configuration the observer is outside the measuring system, i.e. the interferometer is moving relative to the observer while the "ether" is at rest.

Let's calculate the propagation times of the light wave train between beam splitter and mirror 1.

The total distance in the direction of movement ("out") is calculated as follows: While the light wave train travels the distance L with the speed c in the time dt+, the entire structure moves on by v.dt+; the wave train must also cover this distance.

The total optical distance for the "outward journey" then results in:

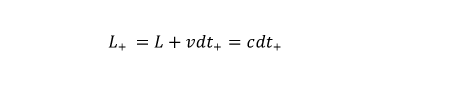
The running time dt+ for the outward journey it is easy to derive:

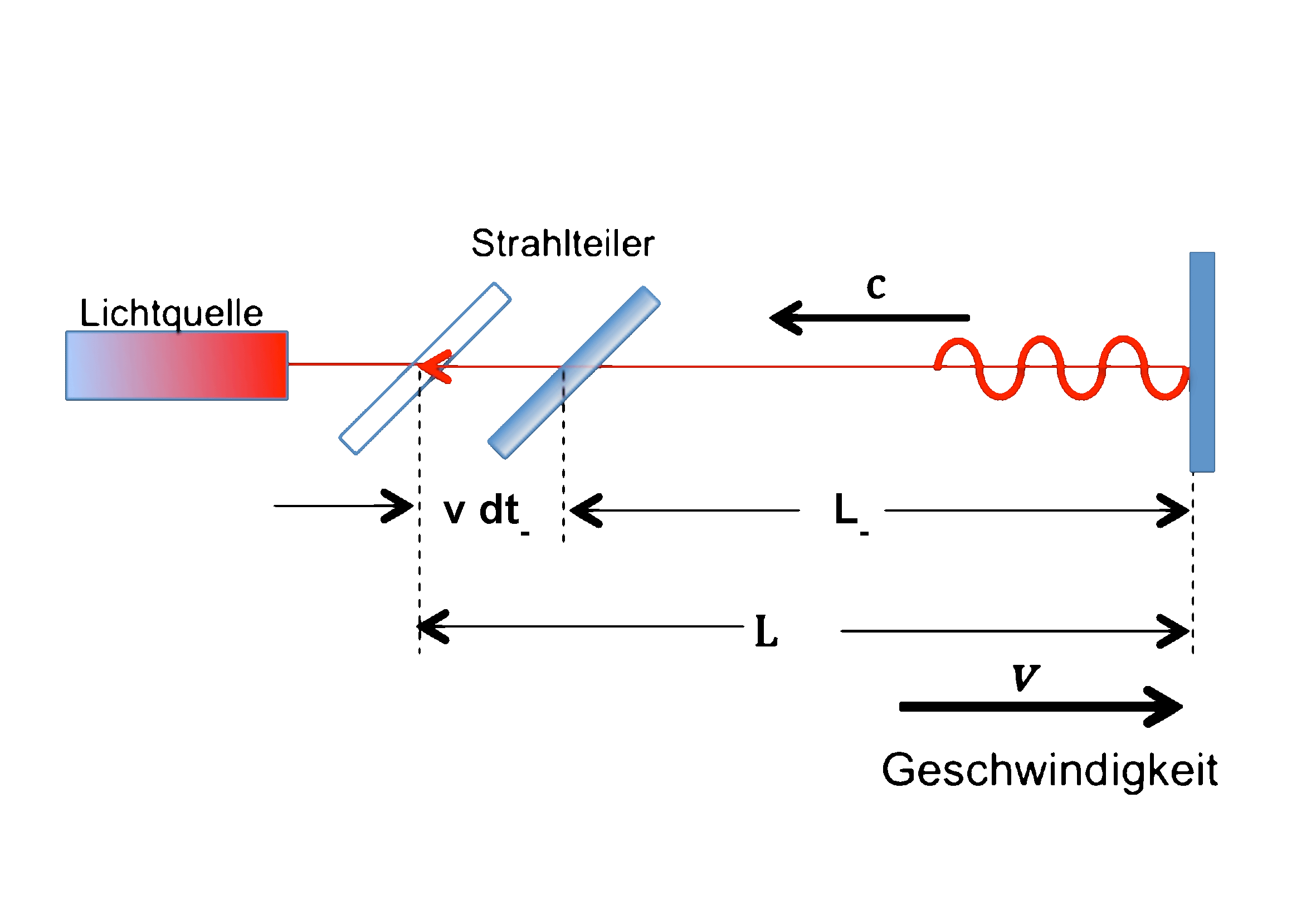
In this case, the beam splitter moves in the opposite direction to the light wave train, so the path L becomes shorter by the distance v.dt-:

.. and this expression is also very easy to solve for the runtime dt-:

The total transit time between beam splitter, mirror 1 and back is now the sum of dt+ and dt-:

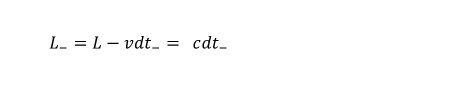
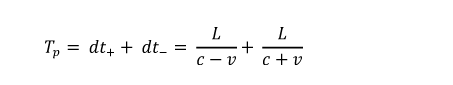
or:

... excuse me for presenting these trivial transformations in such detail here, but I wanted to give you at least the origin of the "famous" show !

"Tp" stands for the total running time (there and back) and the subscript "p" means: parallel to the velocity vector v

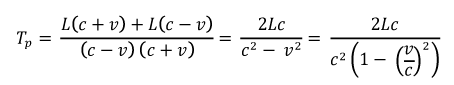
So now we know how long the light wave train is traveling parallel to the direction of movement of the interferometer (beam splitter --> mirror1 --> beam splitter ) both for the observer at rest and for the observer who is moving with us and can - theoretically ! - say something about it , with which speed v the interferometer moves compared to the "ether" postulated by MIchelson. The effect is very small - proportional to (v/c)2 - but it should be measurable! (see below)

Are you actually surprised that the same runtimes result in both cases, although we have chosen very different requirements? Once with (hypothetical) "ether wind", once without! Once with a stationary observer, the other time he is moving!

But it doesn't matter - for a complete description we still have to determine which transit time is to be expected in the direction perpendicular to it (beam splitter --> mirror 2 --> beam splitter).

Before we do that, I should briefly address the question of why Michelson and Morley studied two different transit times: one parallel to the direction of motion (beam splitter --> mirror 1) and one perpendicular to it (beam splitter --> mirror 2) ?

The historical experiment dealt with the question of whether the speed of the earth on its orbit around the sun (approx. 30 km/s !!!) has an influence on the running time.

Since the "transport vehicle earth" cannot simply be stopped to observe the effect of speed, the device was rotated 90 degrees, i.e. the roles of the two running distances were reversed, and Michelson hoped to observe a relative difference between the running times.

I'll explain how this works in detail in a moment.

First of all, there is the question of what total running time (back and forth) is to be expected on the second route perpendicular to the direction of movement.

Here we encounter another difficulty: - how long is the distance perpendicular to the direction of movement?

Just the distance between the beam splitter and mirror 2 ?

Unfortunately it's not that easy. The following sketch shows why:

Sketch from the work of Albert A. Michelson and Edward W. Moreley in 1887

Michelson initially overlooked the fact that the distance perpendicular to the direction of movement of the device also increases proportionally to the speed!

While the light wave train is on its way to mirror 2, the device moves on by the distance v.dts; this increases the walking distance.

According to Pythagoras it can be summed up in the right triangle

(c.dts - v.dts - L ) calculate the side c.dts:

This results in the total running time for the outward and return journey:

This derivation of the signal propagation times Tp and ts can be found in almost all textbooks, but it is extremely problematic!

It remains unclear why the light beam violates the law of reflection when it is reflected at the beam splitter in the direction of mirror 2. The reference by A. Sommerfeld (lectures on theoretical physics, vol. IV, §13, page 61) to the laws of reflection at the moving mirror makes it clear that the frequency of the light wave train also changes, which leads to a beat at the Interferometer output would have to lead.

Incidentally, frequency shifts due to reflection on the moving mirror should also have been taken into account when deriving the transit time Tp! At this point at the latest, the suspicion should arise that the entire classical description of the Michelson effect is "problematic" - but we'll stick with it now, because we're on the same page

1. in good company and

2. Should we not too much at this point Invest "brain wax" because the whole topic will come up later, - from the point of view of the theory of relativity! - turn out to be irrelevant anyway!

Here the question arises whether the runtime effect of the Michelson experiment could not have been increased with a different, slower signal? For example, if we were to use a sound wave instead of light, then with a sound speed of 300 m/s and the same data as above, the transit time difference would be significantly larger, namely: 733 seconds! (We will in chapterdetails for the Sagnac effect investigate the question of whether an alternative to light waves is even possible!)

That should be easy to measure: so why didn't Michelson use a sound wave?

Well, very simple! He wanted to find out about light and not about sound! We'll come back to that.

Now we have all the pieces together to determine the difference between the transit times parallel (Tp) and perpendicular (Ts) to the direction of motion:

If you now consider that the Michelson has rotated its structure by 90 degrees, i.e. the two arms of its device have swapped roles, then the expected runtime difference must be multiplied by a factor of 2.

You can see that we are dealing with a damn small effect! Here's an example; we assume:

Walking distance L = 11 m (roughly like Michelson!details here)
Speed of the Michelson device v = 30 km/s (corresponds to the speed of the earth around the sun)
Speed of light: c = 300,000 km/sec

Do the math - I get a transit time difference of about 2xTo = 7.2 . 10-16 sec

(7.2. 10-16 seconds - you can't measure it with any stopwatch in the world !!! The best atomic clocks have an accuracy of 10-16 seconds! )

How - for God's sake - do you measure such small runtime differences?

Let's take a closer look, maybe there is a chance:

1. Our runtime difference is not about absolute accuracy, but "only" about a relative difference!

2. By using light as a measuring signal, we have the problem because of the high speed of light (c = 300,000 km/s). that the runtime difference is quite small, but because of the short wavelength of approx. 0.5 microns we also have a very fine scale at our disposal!

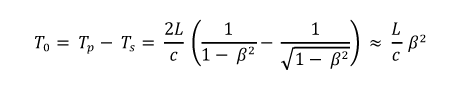
So once again: 7.2.10-16 sec runtime difference corresponds to a runway difference of

d = 2c TO = 2.2.10-7 m = 0.22 microns

At a wavelength of 0.5 microns, this corresponds to a shift of the light wave train by 0.44 wavelengths - and you can easily measure that in the following way:

We imagine the two light signals as a wave train - something like a piece of corrugated iron:

Below, I've represented two light wave trains as two dash patterns for simplicity:

These two light wave trains are now tilted by a very small angle and superimposed (= interfered).
This creates superimposed patterns of light and dark stripes, a so-called "interference stripe pattern"; in this case perpendicular to the course of the wave fronts;

Depending on whether the waves meet in phase ("antinode" on "node") or in phase opposition ("antinode" on "valley"), they reinforce each other or cancel each other out. In the image above, an interference fringe is represented by a wide dark line.

the spacing between the interference fringes varies with the overlap angle between the wave trains; the larger the angle, the closer together the interference fringes - like this:

If the superimposed wave trains are shifted against each other, then the interference fringes are also shifted.
Or more precisely: if the wave trains are shifted by one wavelength, the interference fringes shift by one stripe width.

In the following animation, the upper wave train is shifted back and forth by about 3 "wavelengths" (lines) compared to the lower one; the movement of the wave train is hardly visible, but that of the interference fringe pattern is very good:

More specifically, the superimposition of the wave trains to form an interference fringe pattern in an interferometer looks something like this:

With that we would have found the procedure with which one can measure the tiny transit time or travel distance differences discussed above. A shift of 0.44 wavelengths between the two light trains should result in a shift in the interference fringes of 0.44 fringe widths.

That should actually be very good to watch!

This is exactly what Michelson thought, but when he performed the experiment in 1881 and repeated it in an improved form with Moreley in 1887, he observed

-nothing !!!

So, now we have reached the point where some queer thinkers are still clinging to this day!

Based on Michelson - on very convincing way I think - an effect derived that obviously does not exist at all! And neither for the comoving observer (so.) nor for the dormant (so.)

Michelson himself repeated and refined his experiment until the end of his life (1931), but this did not change the result: a shift in the interference fringes, or some kind of influence of the ether could not be observed with the best will in the world. Similar experiments with constantly improved measurement technology are constantly being repeated to this day (more), the last time in 2009 with a relative accuracy of 10exp-17, but an effect as expected by Michelson cannot be detected.

His contemporaries set up a wide variety of theories to explain this "zero result" or carried out further explanatory experiments - a good summary can be foundhere - but in the end that's all that's leftspecial relativity fromAlbert Einstein with which all phenomena related to the propagation of light known to date can be described without contradiction.

I should perhaps address one particularly striking ambiguity:

At the beginning of this chapter we defined two configurations for the Michelson experiment. -

1. one for the moving observer who hoped to be able to prove an "ether wind" and

2. one for the observer resting outside of the experiment, who tried a kind of race between light wave and

Mirror system to gain information about the speed v of the interferometer.

As you know, the experiment was negative for both configurations! *)

The moving observer concludes that his idea of an "ether" is probably wrong, that there is no such ether and therefore no run-time effect.

But what is the reason why the observer resting outside of the interferometer cannot observe a transit time effect? From the point of view of classical physics, is there no reason why the "race" between the light wave and the reflection of the measuring system - as described above - should not have taken place?

I'll leave this question open - it cannot be answered without contradiction using the means of classical, pre-relativistic physics. But we come in the chapter"Solution - "Sagnac" remains - "Michelson" disappears!" back to it!

*) ... Honestly? Although we have from the point of view of pre-relativitic physics expected runtime effects - like you can also be found in the literature, but I have not yet seen any practical implementation of this experiment with a stationary observer and the moving interferometer known. (If you know of such an experiment, I would be interested in information. PleaseE-mail to me !)

The complete history of all attempts to interpret the Michelson experiment is certainly very exciting and, in addition to a large number of errors and dead ends, also illustrates the mechanisms of human knowledge gain, which are characterized by an intensive search for the "truth" (which actually does not exist), but also of many "right doggednesses".

I do not wish to elaborate further on this "bickering" except for one point which seems to me to be particularly interesting in connection with the Sagnac effect -

Source: Wikipedia

You remember: Michelson was actually looking for the carrier medium of light, the so-called "Ether".

The idea was that the earth, but also the planetary system, rushes through this "ether" at a certain speed and the light wave - similar to sound in moving air - experiences a delay or an entrainment, depending on whether the "ether wind " blows against or in the direction of propagation of the light; he wanted to show that with his interferometer and ultimately prove the existence of this ether.

As already mentioned several times, this has not been possible until today!

But there is an experiment from 1913 with which Georges Sagnac tried to do a similar proof - but this time for rotary movements. In thenext chapter you will see that the classic description of this effect is largely identical to the description of the Michelson effect, but this time the experiment yielded a positive result!

I.e. the same formalism - you will be surprised how extensive the agreement is! - which failed completely in the Michelson experiment, gives exactly the right result in the Sagnac experiment. This was quite irritating for the contemporaries of Michelson and Sagnac and probably also the reason why the critics of the theory of relativity continue to cite this experiment to this day to prove that the Michelson experiment was either carried out incorrectly or misinterpreted and that is why the entire theory of relativity is nonsense! **)

It's time we took a closer look at the Sagnac experiment; here you go further.

___________________________________

**) Perhaps at the end of this report I will be able to resolve the apparent contradiction between "Michelson" and "Sagnac", but to do this we have to be very careful with the terminology used and with "common sense".