
Sagnac, Michelson & Co
Relativität zum "Anfassen"
Rüdiger Rodloff
Hintergrundbild - DLR - Experimental-Laserkreisel - ELSY
Die spezielle Relativitätstheorie - soweit sie zur Beschreibung des Sagnac-Effektes benötigt wird !
Ja, ich weiß: Einführungen in die spezielle Relativitätstheorie gibt es "wie Sand am Meer".
Entweder versuchen die Autoren sich dem Leser anzubiedern, nach dem Motto: "Schaut her ich bin der große Welterklärer - es ist alles ganz einfach", oder sie hüllen sich in den Nebel einer großen Thoerie im Sinne von "Außer mir versteht das sowieso keiner!"
Ich gehöre vermutlich zur ersten Kategorie, ich liebe einfache Erklärungen auch auf die Gefahr hin, dass sich damit (manchmal) unzulässigen Vereinfachungen einschleichen.
Wir haben uns daran gewöhnt, das relativistische Effekte (Zeitdilatation und Längenkontraktion) im Alltag praktisch keine Rolle spielen, weil sie viel zu klein sind. Der optische "Kreisel" ist eines der wenigen Geräte - vielleicht auch die GPS-Navigation ! -, bei dem relativistische Effekte zu einem konkreten "handfesten" und mit "bloßem Auge" zu beobachtenden Resultat führt !
"erklären" ist hier das völlig falsche Wort !
ERKLÄRUNG bedeutet laut Wikipedia die Nennung der Ursachen eines Phänomens; eine ERKLÄRUNG überzeugt, leuchtet ein oder sie ist zufriedenstellend.
Alles das leistet die Feststellung, dass die Lichtgeschwindigkeit eine Konstante in allen Bezugssystemen ist gerade nicht !
Aber es ist nicht wichtig, ob uns diese Feststellung einleuchtet, oder ob sie uns überzeugt - wichtig ist allein: Lassen sich mit dieser Feststellung die Beobachtungen in der Natur beschreiben, oder nicht.
Also los, - wie wollen wir uns der Sache nähern ?
Wir sollten uns zunächst die beiden Grundpostulate der Relativitätstheorie ansehen und anschliessend untersuchen, ob damit die experimentellen Ergebnisse zufriedenstellend erklärt werden können:
Postulat 1. In allen gleichförmig gegeneinander bewegten Systemen gelten durchweg die gleichen Naturgesetze.
Postulat 2. Die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante.
Postulat 1 ist das bereits von Galilei und Netwon erkannte Relativitätsprinzip, - hier allerdings in der Formulierung von A. Einstein.
Postulat 2 ist das Ergebnis einer Jahrhunderte langen Suche nach dem Wesen des Lichtes bzw. der elektromagnetischen Wellen.
Tausende von Experimente über die Natur des Lichtes vor und nach Einstein sind nicht anders als mit der Feststellung zu erklären, dass das Licht sich immer und überall mit der gleichen Geschwindigkeit ausbreitet; Einstein hat deshalb das Relativitätsprinzip von Galilei um diesen Punkt erweitert.
So, was ist damit nun in der Praxis gemeint -
zunächst zu Postulat 1 - Galilei's Relativitätsprinzip:
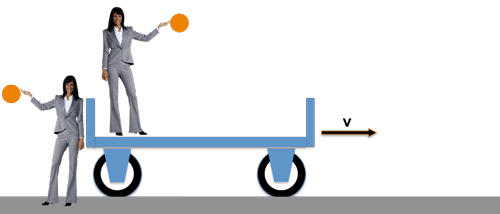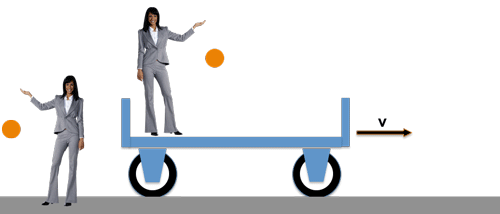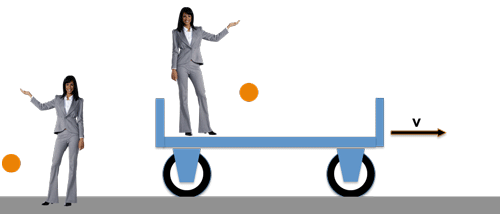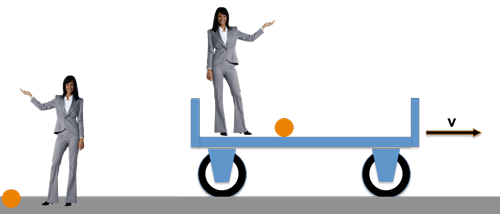
Das gilt übrigens auch auch für Experimente aus dem Bereich der Elektrodnymik, Optik, Thermodynamik u.s.w., denn gerade das ist ja die Aussage des Relativitätsprinzips von Galilei:
>> In allen gleichförmig gegeneinander bewegten Systemen gelten durchweg die gleichen Naturgesetze <<
Die Dame auf dem Wagen bewegt sich mit der gleichförmigen Geschwindigkeit v gegenüber der anderen Dame auf dem Bahnsteig. Beide führen ein Fallexperiment durch und beide beobachten exakt dasselbe: die Kugel fällt aus derselben Höhe in derselben Zeit geradlinig nach unten - denn für beide gilt ja dasselbe Fallgesetz !
Die Dame auf dem Wagen, wird in ihrem "Bezugssystem" keinerlei Auswirkung der Wagenschwindigkeit v auf die Bewegung der Kugel erkennen können .....
..... und die Dame auf dem Bahnsteig hat ohnehin keine Grund an der Gültigkeit ihrer Beobachtung zu zweifeln, obwohl ihr "Bezugssystem", nämlich der Bahnsteig, zusammen mit der Erde eigentlich auch ganz schön schnell unterwegs ist !
Soweit das klassische Relativitätsprinzip-Postulat 1.
Dieser Vergleich der verschiedenen Ausbreitungsgeschwindigkeiten, z.B. von Licht-, Wasser- ,Schallwellen oder gar Geschossen und Wasserstrahlen ist sehr problematisch und im Grunde sogar falsch:
--> hier werden nämlich Äpfel mit Birnen verglichen:
Die Geschwindigkeit einer Kanonenkugel, oder eines Wasserstrahls wird natürlich auch von der Geschwindigkeit der "Quelle" beeinflußt; die Mündungsgeschwindigkeit und eine eventuelle Bewegung des Geschützes addieren sich natürlich zu einer Gesamtgeschwindigkeit.
Bei einer Schallwelle ist das ganz anders: deren Ausbreitungsgeschwindigkeit hängt nur von den Eigenschaften des Trägermediums ab und ist vollkommen unabhängig von der Geschwindigkeit der Quelle - wie man sehr gut an Überschallflugzeugen beobachten kann. Hier "überholt" die Quelle (das Flugzeug) sogar die eigene Welle !
_-_filtered.jpg)
Totzdem gilt natürlich auch bei der Schallausbreitung die Additivität der Geschwindigkeiten, wir müssen nur sauber unterscheiden wer bzw.was sich gegenüber wem bewegt. Im Fall der Schallausbreitung geht es um die Relativbewegung zwischen Trägermedium und Beobachter !
Festzuhalten bleibt:
Licht "benimmt" sich, was seine Ausbreitungs-geschwindigkeit betrift, nicht wie ein Geschoss und man konnte auch nie ein Trägermedium wie beim Schall nachweisen.
Manche Experimente sprechen dafür, das Licht eine Transversalwelle ist (Polarisation), andere sind nur durch eine Teilchenvorstellung (Photoeffekt) zu erklären.
Was also ist Licht ? Seit Einstein haben die (meisten!) Physiker die Versuche eingestellt diese Frage zu beantworten; wir nehmen die verschiedenen Effekte und Erscheinungsformen zur Kenntnis - und fertig!
Postulat 2. Die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante.
Nun kommen wir zum zweiten Teil des "speziellen" Relativitätsprinzips:
Die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante.
Was bedeutet das konkret ?
Wir stellen uns dazu 'mal den folgenden Versuchsaufbau vor:
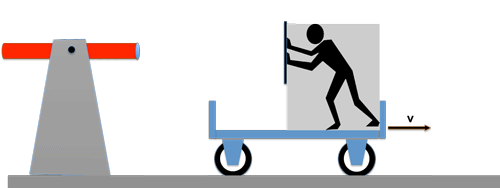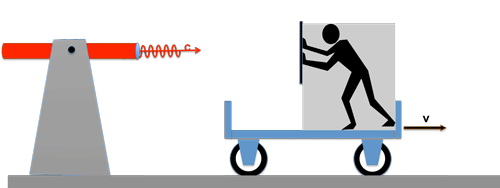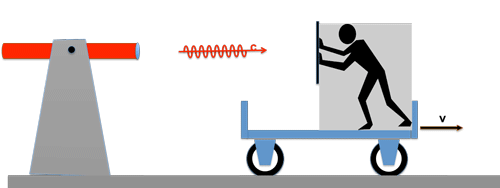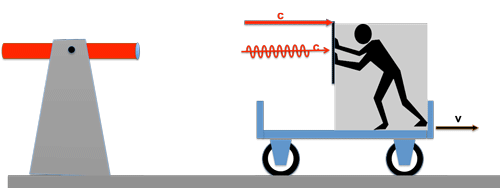
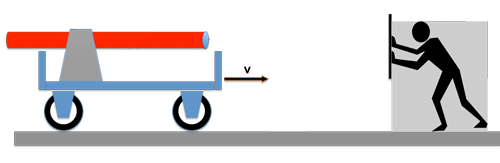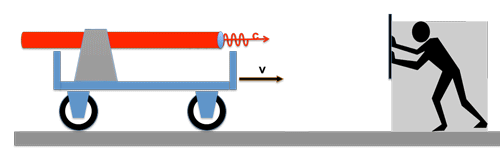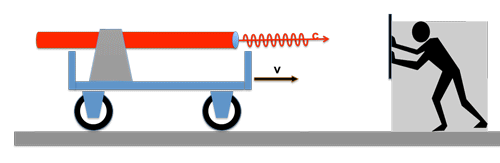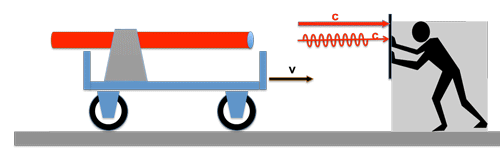
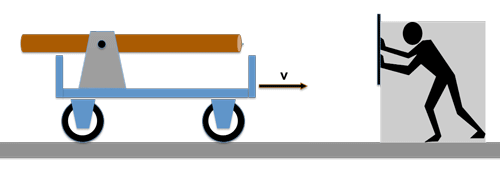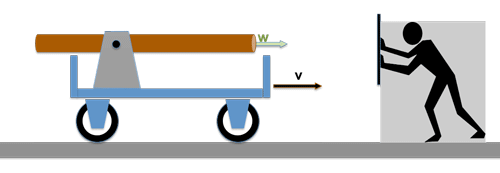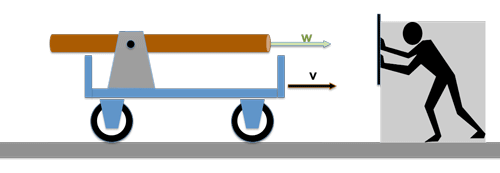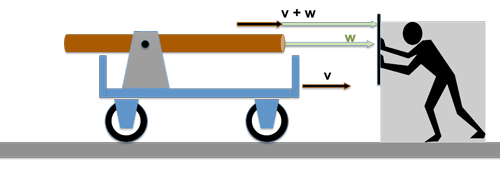
Von einer ruhenden Lichtquelle wird ein Lichtwellenzug mit der Geschwindigkeit c einem fahrenden Wagen hinterher geschickt; der Wagen hat die Geschwindigkeit v.
Auf dem Wagen befindet sich ein Beobachter, der den Auftrag hat, die Geschwindigkeit des eintreffenden Lichtstrahls zu messen. Wie er das macht soll uns im Momemt nicht kümmern ! Was glauben Sie, wird das Ergebnis seiner Messung sein ? --> Richtig: die Geschwindigkeit des Lichtes ist nach wie vor c !
Egal wie schnell der Wagen fährt, für den Beobachter auf dem Wagen bleibt die Lichtgeschwindigkeit immer dieselbe!
Drehen wir die Situation mal um:
Jetzt montieren wir die Lichtquelle auf einen Wagen und lassen denselben mit der Geschwindigkeit v auf den Beobachter zufahren. Auch jetzt wird sich für den Beobachter nichts ändern: er wird noch immer die gleiche Geschwindigkeit c des Lichtwellenzuges messen wie vorher !
Stellen Sie sich doch mal vor, wir hätten die obigen Experimente nicht mit einen Lichtquelle, sondern mit einer Wasserspritze durchgeführt. Die Geschwindigkeit des Wasserstrahls sei w.
Das Ergebnis der Geschwindigkeitsmessungen für den Wasserstrahl wäre ganz anders ausgefallen; die Geschwindigkeit v des Wagens hätte sich deutlich bemerkbar gemacht: --> Im ersten Fall wäre der Wasserstrahl mit einer Geschwindigkeit (w-v) auf dem Wagen eingetroffen, im zweiten Fall, würde der ruhende Experimentator von einem Wasserstrahl der Geschwindigkeit (w+v) getroffen werden.
Die Aussage "die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante"
bedeutet:
--> für das Licht gilt die herkömmliche Addition der Geschwindigkeiten nicht !
Egal ob sich Sender und / oder Empfänger gegenander bewegen oder nicht, oder ob sich der Empfänger gegenüber einem (hypothetischen) Trägermedium dem "Äther" bewegt oder nicht, die (Vakuum-) Geschwindigkeit des Lichtes bleibt immer gleich !
Und bitte nicht verwechseln -
die Geschwindigkeit bleibt konstant, - nicht aber die Frequenz !
Die Feststellung, dass die Lichtgeschwindigkeit in jedem Bezugssystem konstant ist, ist mit dem "gesunden Menschenverstand" und/oder der "Anschauung" nicht zu fassen, aber Sie werden sehen, dass sich mit dieser Annahme tatsächlich sämtliche experimentellen Befunde erklären lassen. (Etwas schlaueres ist uns eben bislang noch nicht eingefallen!)
Hier nochmal die beiden Postulate der Relativitätstheorie:
1. In allen gleichförmig gegeneinander bewegten Systemen gelten durchweg die gleichen Naturgesetze.
und
2. Die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante.
Bevor wir uns überlegen, wie sich die beiden Prinzipien miteinander "verheiraten" lassen, müssen wir noch einen Schritt weitergehen:
Bislang haben wir uns lediglich darum gekümmert, wie sich die Situation innerhalb des jeweiligen Systems darstellt. Wir haben festgestellt, dass die gleichen physikalischen Gesetzmäßigkeiten gelten und wir haben uns damit abgefunden, dass ein Lichtwellenzug immer die die gleiche Geschwindigkeit hat, - egal wo sich die Quelle befindet, oder mit welcher Geschwindigkeit sie sich relativ zum jeweiligen Bezugssystem bewegt; das gefällt uns zwar nicht und verursacht Krämpfe in der Welt unserer Alltagserfahrung, aber die experimentelle Realität ist nun einmal so!
Im Grunde ist alles ganz einfach, solange wir unser Bezugssystem - z.B. den gleichmäßig dahin rollenden Eisenbahnwagen - nicht verlassen:
--> Es gelten immer die bekannten Naturgesetze und wenn uns ein Lichtstrahl begegnet, dann hat er immer die gleiche Geschwindigkeit egal ob er von einer bewegten oder einer ruhenden Quelle ausgesandt wird!
So weit so einfach !
In der speziellen Ralativitätstheorie geht es aber um eine etwas weitergehende Frage, - die Frage nämlich, wie eine physikalische Gesetzmäßigkeit, z.B. ein Bewegungsablauf, zu beschreiben ist, wenn sie von einem zweiten Bezugssystem beobachtet wird und beide Bezugssysteme sich relativ zueinander mit einer gleichförmigen Geschwindigkeit bewegen. (Daher der Name "Relativitäts"theorie !)
Das hört sich etwas theoretisch an. Zur Verdeutlichung sollten wir zu unserem ersten Beispiel mit den "fallenden Kugeln" zurückkehren:
Sie erinnern sich: die Fallgesetze sind in einen ruhenden Bezugssystem genau die gleichen, wie in einem gleichförmig bewegten System (Eisenbahnwagen oder Schiff); so weit so klar !
Sie werden das Fallgesetz aber nicht wiedererkennen, wenn wir den Experimentator bitten, das Experiment von "außen", aus einer "ruhenden" Position zu beobachten, z.B. mit einem Fernglas. Jetzt könnte der Weg der fallenden Kugel in etwa so aussehen:
Bitte entschuldigen Sie die etwas unbeholfene Animation!

Das ist nicht neu und bereits seit Galilei bekannt.
Achtung: das ist die entscheidende Aussage !
Für den Beobachter außerhalb des Wagens fällt die Kugel keineswegs geradlinig nach unten; sie bewegt sich mit dem Wagen und durchläuft soetwas wie eine Wurfparabel. Der Beobachter außerhalb des Wagens könnte aus der Flugbahn der Kugel auf die Geschwindigkeit des Wagens v schliessen. Für den Beobachter im Wagen ist das nicht möglich, für ihn fällt die Kugel nach wie vor senkrecht nach unten !
Es ist also ein großer Unterschied ob wir ein Experiment "innerhalb" eines gleichförmig bewegten Bezugssystem beobachten, oder von "außen", d.h. von einem zweiten, relativ zum ersten ruhenden System.
Und jetzt kommt der entscheidende neue Schritt:
Wir wollen jetzt die Sache mit der konstanten Lichtgeschwindigkeit ins Spiel bringen, d.h. wir sollten uns Situationen ansehen, bei denen das Licht eine Rolle spielt !
Wenn die Lichtgeschwindigkeit immer gleich ist, d.h wenn das Licht sich dem "normalen" Additionsgesetz für Geschwindigkeiten "entzieht", dann muß man erwarten das sich auch die Längen und Zeitmessung innerhalb des relativ bewegten Systems ändert und zwar in dem Sinn, dass das Additionsgesetz für die (Vakuum)-Lichtgeschwindigkeit nicht mehr gilt und für die Addition sehr hoher Geschwindigkeiten eine Art Übergangslösung existiert.
Das klingt reichlich kryptisch und: JA, Sie haben recht: das ist auch schwer vorstellbar!
Nehmen wir uns zunächst 'mal die Zeitmessung vor!

Die Zeitdilatation.
Da gibt es z.B. die berühmte "Lichtuhr":
Die Grundidee ist eigentlich genial !
Wenn die Lichtgeschwindigkeit immer und überall konstant ist, dann könnte man das doch hervorragend ausnutzen um daraus eine extrem stabil laufende Uhr zu konstruieren!
Dazu lassen wir einen Lichtpuls ständig zwischen zwei Spiegeln hin und her laufen und jedesmal, wenn der Lichtpuls wieder an seinem Ausgangspunkt ankommt springt ein Zähler einen Schritt weiter.
Bei einer Geschwindigkeit c des Lichtes und dem Abstand LE zwischen den Spiegeln beträgt die Laufzeit
tE = LE / c
Als nächstes montieren wir diese "Lichtuhr" auf einen Wagen, der mit der Geschwindigkeit v unterwegs ist.
Für den mitfahrenden Beobachter ändert sich dadurch nichts:
Die "Lichtuhr"
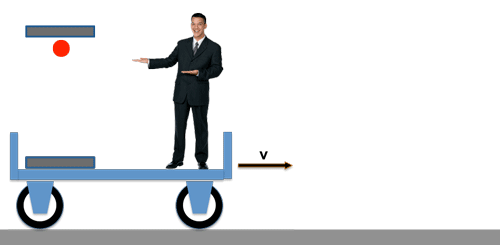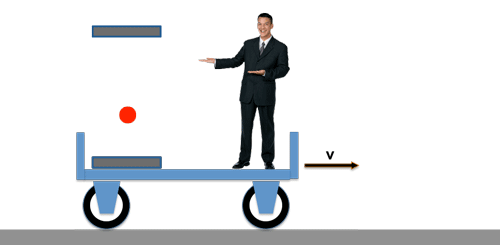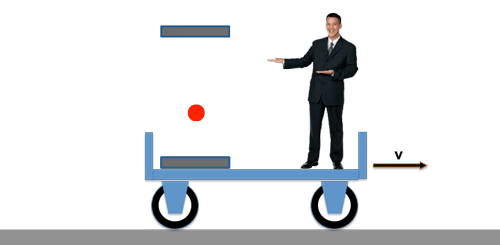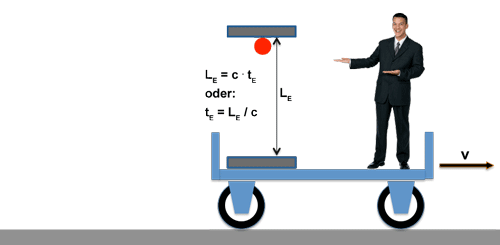
Die Laufzeit des Lichtes zwischen den Spiegeln - und damit die Taktfrequenz unserer "Lichtuhr" - beträgt nach wie vor:
tE = LE / c
Im nächsten Schritt lassen wir den Beobachter am Strassenrand stehen, alles andere bleibt aber so wie es war. Für den ruhenden Beobachter nimmt das Experiment jetzt aber einen völlig anderen Verlauf:

Wie gesagt: - wir haben an der "Lichtuhr" überhaupt nichts verändert. Lediglich die Beobachterposition ist eine andere und genauso wie bei unserem Fallexperiment oben, nimmt der Lichtwellenzug jetzt einen ganz anderen Weg. Da die Lichtgeschwindigkeit im Gegensatz zur Geschwindigkeit der fallenden Kugel konstant ist, verläuft das Licht auf einem geradlinigen Zick-Zack-Weg und nicht auf einer gekrümmten Wurfparabel, - das braucht uns im Augenblick aber nicht weiter zu interessieren.
Viel spanndender ist die folgende Frage:
Funktioniert unsere "Lichtuhr" für den ruhenden Beobachter genauso wie für den mitfahrenden? Hat sich eventuell die Taktfrequenz geändert ?
Dazu müssen wir uns die Situation 'mal etwas genauer ansehen und die vom Licht LE und vom Wagen LW zurückgelegten Wege analysieren:

LE = c . tE ist der Weg der Lichtwelle aus der Sicht des mitfahrendes Beobachters;
LR = c . tR ist der Weg der Lichtwelle aus der Sicht des ruhenden Beobachters;
LW = v . tR ist der Weg des Wagens aus der Sicht des ruhenden Beobachters;
Wir brauchen an dieser Stelle eigentlich garnicht weiterrechnen:
Sie können sehr leicht erkennen, dass der Weg der Lichtwelle aus der Sicht des ruhenden Beobachters LR länger ist als der Weg aus der Sicht des mittfahrenden Beobachters LE und wenn der Weg länger ist, benötigt die Lichtwelle mehr Zeit, kurz und gut: für den ruhenden Beobachter geht die Lichtuhr langsamer !
Aber um den Anschluß an die Standardliteratur zu finden, können wir diese Einsicht auch noch mit etwas Trivialmathematik garnieren:
Das Ganze ist ein rechwinkliges Dreieck und wir können den Satz des Pythagoras anwenden:
und die obigen Beziehungen für die Laufwege LE, LW und LR einsetzen:
nach der Eigenzeit des mitfahren Beobachters tE aufgelöst ergibt sich:
...durch eine simple Umstellung der Gleichung ....
Oder in der etwas bekannteren Schreibweise:
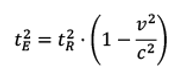

Was ist hier eigentlich gerade passiert ?
Wir haben den Standort gewechselt und schon gehen die Uhren langsamer !
Wieso ?
An welcher Stelle ist in unsere Rechnung dieser Effekt hineingeruscht ?
Wir haben doch nur eine ganz simple Dreiecksberechnung für die Laufwege LE, LR und LW durchgeführt!
Nochmal - wo liegt der "Knackpunkt" ?
Die Antwort ist ebenso simpel wie unsere ganze Rechnung:
Wir haben die Signal- bzw. Lichtgeschwindigkeit c konstant gehalten,- ist das eigentlich richtig ? Aus der Sicht der normalen Alltagsmechanik eigentlich nicht!
Überlegen Sie doch 'mal:
- aus der Sicht des mitbewegten Beobachters auf dem Wagen beträgt die Geschwindigkeit des Lichtpulses zwischen den Spiegeln c - das ist klar !
- aus der Sicht des ruhenden Beobachters haben wir für die Geschwindigkeit des Lichtpulses ebenfalls c angesetzt, getreu dem Relativitätsprinzip "Die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante" .
Aber nach unserer "Alltagserfahrung" hätten wir aus der Sicht des ruhenden Bobachters für die Signalgeschwindigkeit auch noch die Geschwindigkeit v des Wagens berücksichtigen müssen ! Wenn wir das tun, ist der ganze Spuk verschwunden!
Die Sache mit der langsamer gehenden Uhren ergibt sich also sehr direkt aus dem Postulat:
>> die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante <<
Im folgenden Abschnitt führen wir die ganze Rechnung noch einmal durch, diesmal allerdings berücksichtigen wir bei der Signalgeschwindigkeit auch noch die Wagengeschwindigkeit v und Sie werden sehen, das von der Zeitdilatation nichts bleibt.
Sie können den folgenden Abschnitt aber auch einfach überspringen - er zeigt nämlich nur, das unsere Alltagsmechanik bei der Herleitung der experimentell nachgewiesenen (!) Zeitdilatation versagt.
"Zeitdilatation" - aus klassischer Sicht
Aus der Lichtgeschwindigkeit c und der Wagengeschwindindigkeit v ergibt sich (aus der Sicht des ruhenden Beobachters !) die resultierenden Geschwindigkeit c'. (s.o.)
Die lässt sich mit Hilfe der Pythagoras-Beziehung sehr leicht berechnen:
die Beziehungen für Laufwege LE, LR und LW lauten:
Für die Laufwege gilt ebenso wie für die Geschwindigkeiten der Satz des Pythagoras:
Für LR müssen wir allerdings bedenken, daß wir jetzt die die Signalgeschwindigkeit c' einsetzen müssen:
Mit der obigen Beziehung ergibt sich daraus:
oder: tE = tR
bzw. in Worten: Eigenzeit im Bezugssystem = Zeit des Ruhesystems
d.h. wenn man die klassische Additivität von Geschwindigkeiten voraussetzt, dann ist die Zeit im Ruhesystem identisch mit der Zeit im dazu relativ bewegten System (Bezugssystem).
Die beiden Uhren gehen gleich - der Zeitdilatationeffekt ist verschwunden !
c : Signal- / Lichtgeschwindigkeit
v : Wagengeschwindigkeit
c' : Signalgeschwindigkeit aus der Sicht
des ruhenden Beobachters
LE : Laufweg im bewegten System
LW : (Lauf-) Fahrweg des Wagens
LR : Laufweg aus der Sicht des
Ruhesystems


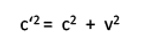

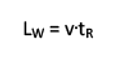

tE : Eigenzeit im bewegten Bezugssystem
tR : Zeit aus der Sicht des Ruhesystems


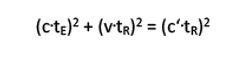
'tschuldigung, das Beispiel ist nicht gerade orginell; mir ist halt nichts besseres eingefallen!
Die Längenkontraktion
Die Tatsache, dass wir die Lichtgeschwindigkeit grundsätzlich und überall als konstant annehmen müssen, zwingt uns dazu auch noch weitere Elemente unserer Alltagsmechanik neu zu definieren, - z.B. die Länge eines bewegten Körpers oder die Länge einer Strecke ... und wir müssen auch hier sehr genau unterscheiden von wo wir den Vorgang beobachten.
.
Wir wollen 'mal ein Beispiel betrachten:
Eine Rakete startet von der Erde, sagen wir: zum Mond.
Für den Beobachter auf der Erde - dem "Ruhesystem" - sieht das so aus:
- LR istdie Strecke die die Rakete zurücklegt ;
- tR ist die Zeit die dabei verstreicht
- v ist die Geschwindigkeit der Rakete.
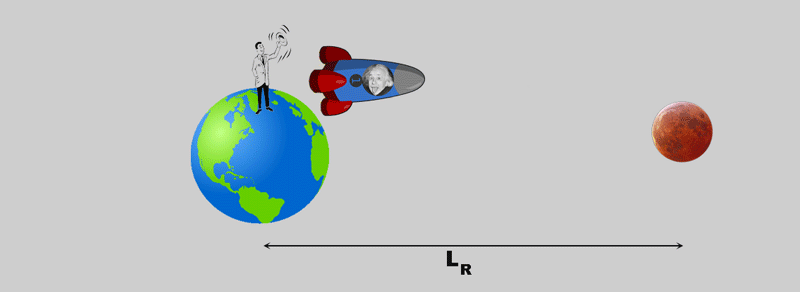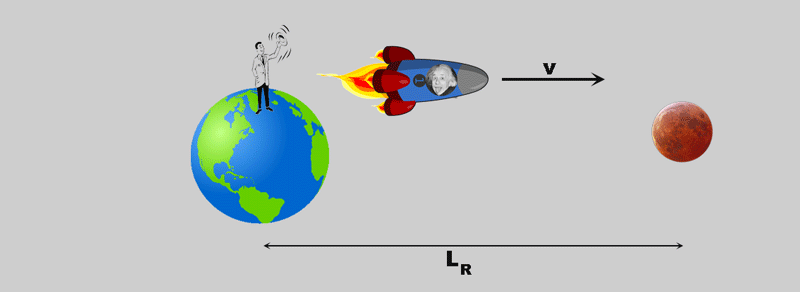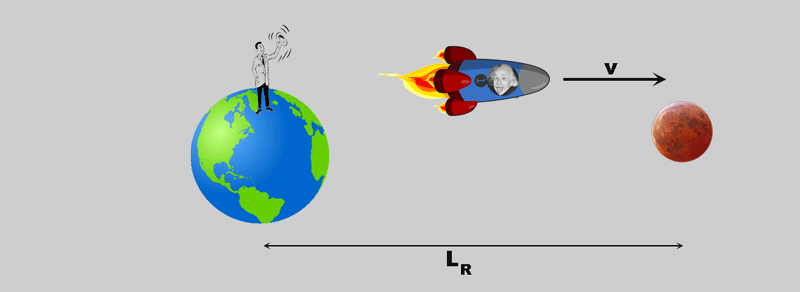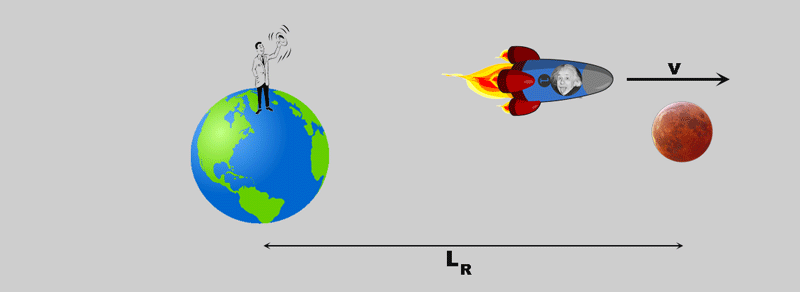
Der Beobachter in der Rakete hat einen etwas anderen Eindruck vom Geschehen:
- das "Ruhesystem" (Erde-Mond) bewegt sich unter ihm hinweg;
- aus seiner Sicht legt er Strecke LE zurück;
- die Zeit die dabei verstreicht ist tE;
Bezüglich der Geschwindigkeit mit der sie sich gegeneinder bewegen sind sich die beiden Beobachter auf der Erde und in der Rakete aber einig, - die beträgt v !

Was war noch unser Ziel ..... ?
... zur Erinnerung:
Wir sind dabei zu untersuchen, ob sich Wegstrecken (in unserem Beispiel LR und LE) jeweils aus der Sicht des ruhenden bzw. des bewegten Beobachters unterscheiden und wenn ja: um wieviel.
Dazu haben wir bereits alle Informationen beieinander, - wir müssen sie nur noch ordnen. Los geht's:
Die Geschwindigkeit der Rakete aus der Sicht des ruhenden Beobachters ist:
v = LR / tR
Die Geschwindigkeit der Rakete aus der Sicht des mitbewegten Beobachters ist:
v = LE / tE
Da für beide Beobachter die Geschwindigkeit v gleich sein muß gilt:
LE / tE = LR / tR
oder:
LE = LR . (tE/tR)
Den Zusammenhang zwischen der Eigenzeit tE im bewegten System (der Rakete!) und der Zeit tR im Ruhesystem (auf der Erde !) kennen wir bereits (s.o.):
mit
Wenn wir diesen Ausdruck in die obige Beziehung für LE einsetzen, dann erhalten wir:
oder:
d.h. aus der Sicht des bewegten Beobachters ist Strecke LR (zwischen Erde und Mond) um den Faktor verkürzt - das ist die sog. Längenkontraktion !


In unserer Alltagsmechanik hat das allerdings keine allzu große Bedeutung; ein Beispiel:
Nehmen wir ein Auto, dass mit 100 km/h fährt . Für den Beobachter am Strassenrand wird deshalb die Uhr im Auto um den Faktor: 0,999 999 999 999 995 langsamer laufen als seine eigene; d.h. nach ca. 3,5 Millionen Jahren zeigen die beiden Uhren Uhren einen Unterschied von 1 Sekunde !
Wenn das "Auto" allerdings mit der halben Lichtgeschwindigkeit ( 150 000 km/sek) unterwegs ist, dann beträgt der Korrekturfaktor 0,866.
Jetzt zeigen die beiden Uhrten bereits nach 7 Sekunden einen Gangunterschied von 1 Sekunde!
Aber Autos die 150 000 km/sek schnell sind gibt es noch nicht ;-) ... und selbst die schnellste Rakete (Helios 1 und 2) ist mit ca 70 km/sek noch keine Konkurrenz für das Licht !
So, wir haben jetzt die ersten und wohl auch bekanntesten Elemente der speziellen Relativitätstheorie beieinander:
- die Zeitdilatation - bewegte Uhren gehen langsamer !
und
- die Längenkontraktion - die Streckenlänge in relativ bewegten Systemen verkürzen sich
... und nochmal zur Erinnerung:
Wir mußten diese Korrekturen in der Längen- und Zeitmessung einführen, um die Bedingung zu erfüllen, dass die Lichtgeschwindigkeit c grundsätzlich und überall, in allen beliebig gegeneinander bewegten Systemen immer konstant ist !
Ich denke das war bislang nicht allzu schwierig, - wir müssen nur den Gedanken einer in allen Bezugssystemen konstanten Lichtgeschwindigkeit konsequent zu Ende denken und schon landen wir bei der Zeitdilatation und der Langenkontraktion !
Aber leider - das Ganze war bislang nur eine "Fingerübung", denn wenn wir das Michelson- und das Sagnacexperimentes richtig verstehen wollen, dann müssen wir noch einen Schritt weiter gehen:
--> wir müssen verstehen wie sich die Geschwindigkeit eines Signals berechnet, wenn sich diese aus zwei Teilgeschwindigkeiten zusammensetzt.
Hier das (etwas plumpe) Beispiel: Ein kleiner Wagen auf einem großen Wagen.
- Ein Trägerwagen fährt mit der Geschwindigkeit v
- Auf dem Trägerwagen befindet sich ein weiterer Wagen der sich (gegenüber den Trägerwagen) mit der Geschwindigkeit u bewegt; ein ruhender Beobachter wird dann folgendes sehen:
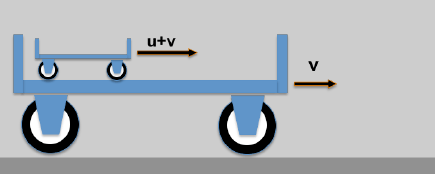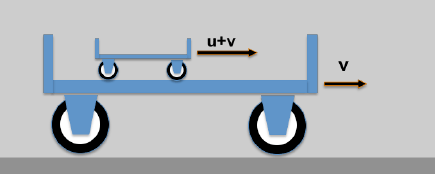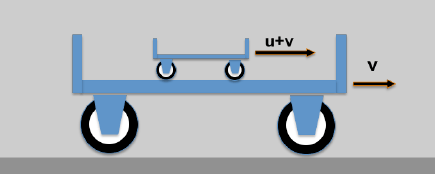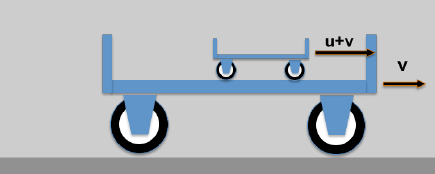
*) 10-4c sind 30 km/sek; das entspricht der Geschwindigkeit der Erde auf ihrer Umlaufbahn um die Sonne!
Wir reden hier immer von der Vakuumlichtgeschwindigkeit c !
Anforderungen an ein Additionstheorem für Geschwindigkeiten:
Die resultierende Geschwindigkeit des kleinen Wagens würde ein Beobachter (der noch nie etwas von der Relativitätstheorie gehört hat) mit w = u + v angeben.
"Na und" .... werden Sie sagen, "warum erzählt er uns das ? Das ist doch trivial!"
Ich muß Sie enttäuschen: die "Addition" von Geschwindigkeiten die wir gerade praktiziert haben ist leider überhaupt nicht trivial und für sehr große Geschwindigkeiten - in der Nähe der Lichgeschwindigkeit c - ist der obige Ausdruck ( w= u + v ) sogar richtig falsch !
Nehmen wir wieder ein Beispiel:
Die Geschwindigkeit des Trägersystems ( das kann z.B ein optisches Gerät sein) sei
10-4 c *); in diesem Gerät läuft ein Lichtwellenzug mit der Geschwindigkeit c .
Für einen ruhenden Beobachter würde die resultierende Geschwindigkeit nach der klassischen Additionsmethode dann
1,00001.c
betragen, - also über der Lichtgeschwindigkeit c liegen, was nicht sein kann - denn die Lichtgeschwindigkeit ist eine Grenzgeschwindigkeit und
.... die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante!
(s.o. - 2. Postulat!)
Wir müssen also ein Additionstheorem für Geschwindigkeiten finden, das die folgenden Eigenschaften hat:
1. Die resultierende Geschwindigkeit darf niemals größer als die Lichtgeschwindigkeit c sein;
2. Für kleine Geschwindigkeiten sollte (näherweise) das klassische Additionstheorem
( w = u+v ) gelten.
Also gut: Michelson wollte letztlich nicht die Geschwindigkeit seines Interferometers bestimmen, sondern die Existenz eines Trägermediums für Lichtwellen , den sog. Äther, nachweisen, aber auch dazu mußte er die Signalgeschwindigkeit kennen.
Warum ist das gerade für das Sagnac-Interferometer so wichtig?
Mit dem Gerät soll die Laufzeit von (Licht-)Signalen gemessen werden und zwar in einem (Träger-)System das sich seinerseits mit einer bestimmten Geschwindigkeit bewegt, bzw. rotiert. Ziel der Experimente ist es aus der Laufzeit des Lichtsignals auf die Bewegung bzw. die Geschwindigkeit des Trägersystems zu schliessen !
Um hier keinen Fehler zu machen müssen wir sehr genau untersuchen, wie sich für den ruhenden Beobachter (!) die Geschwindigkeit des Trägersystems (=Interferometers) und die Signalgeschwindigkeit zusammensetzt.

Sie kennen diese kleinen Skizzen inzwischen zur Genüge - was sehen Sie ?
- ein ruhender Beobachter steht neben einem Trägersystem, das sich relativ zu seiner Position mit der Geschwindigkeit v bewegt;
- auf dem Trägersystem befindet sich eine Quelle, die relativ zum Trägersystem ein Signal mit der Geschwindigkeit c aussendet;
- der Beobachter kennt die Signalgeschwindigkeit c und möchte aus der Laufzeit des Signals über eine bestimmte Strecke die Geschwindigkeit v des Trägersystems ermitteln;
- er muß dazu die Frage beantworten, mit welcher Geschwindigkeit sich das Signal aus seiner Sicht ausbreitet.
In der klassischen Physik hätte er dazu die Geschwindigkeit des Trägersystems v und die Signalgeschwindigkeit c addiert, - aber wir wissen ja, dass das unter dem Gesichtspunkt des 2. Postulates ( die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante !) falsch ist.
Keine Angst - wir haben bereits soviel Grundlagenwissen, dass wir trotzdem recht schnell zum Ziel kommen! Es hilft also nichts, wir müssen uns mit der Frage beschäftigen wie Geschwindigkeiten vor dem Hintergrund der zwei relativistischen Postulate zu addieren sind und wie üblich, fangen wir dafür - wieder einmal - ganz von vorne an!
Galileitranformation
Womit beschäftigt sich die Relativitätstheorie ?
Kurz und knapp - es geht um relativ gegeneinander bewegte Bezugssysteme - daher der Name ! - und den Einfluß dieser Bewegung auf physikalische Größen.
Wir haben bereits festgestellt, dass wir die Zeitmessung und die Längenmessung korrigieren müssen, wenn sich das betreffende Bezugsystem mit einer konstanten Geschwindigkeit bewegt.
Wir wollen uns nun die Frage stellen, wie man die Koordinaten des ruhenden Bezugssystems in die des bewegten umrechnen kann und wir fangen zunächst mal mit den klassischen Ansatz an:
Die Galilei-Transformation
... und weil wir uns das Leben so einfach wie möglich machen wollen, liegen die Koordinatenachsen der beiden Bezugssysteme parallel zueinander und die Bewegungrichtung verläuft genau in Richtung der x-Achse, etwa so wie in diesem
Beispiel:

Wenn sich das bewegte Bezugssysten (x', y', z') mit der Geschwindigkeit v in Richtung der x-Achse bewegt, dann legt es in der Zeit t' den Weg v.t' zurück - und zwar in x-Richtung. D.h. der Zusammenhang der x- und der x'-Koordinate lässt sich ganz einfach so darstellen:
x = x' + v.t'
Durch Vertauschung der Koordinatenn x und x', bzw. t und t' kann auch die Position des Beobachters vom ungestrichenen in das gestrichene Bezugssystem verschoben werden; dabei muß allerdings das Vorzeichen der Geschwindigkeit v gewechselt werden - ich denke das ist anschaulich klar.
x' = x - v.t
(Formal lösen wir die obige Gleichung einfach nach x' auf!)
Für die anderen Koordinaten bleibt alles beim alten:
y = y'
z = z'
und natürlich ändert sich auch nichts an der Zeit:
t = t'
Aus unseren Betrachtung zur Längen- und Zeitmessung in bewegten Systemen (s.o.) wissen wir aber, dass bewegte Uhren anders gehen - nämlich langsamer - und das sich die Strecken in Bewegungsrichtung verkürzen !
Diese Effekte werden durch die Galileitransformation aber nicht erfasst.
D.h. wir müssen und um eine allgemeingültigere Transformation kümmern!
Zunächst sollten wir uns aber überlegen, welche Eigenschaften diese neue Transformation haben muß:
1. Die Transformation muß linear sein, d.h. die Transformation muß gerade, gleichförmige Bewegungen wieder auf gerade, gleichförmige Bewegungen abbilden.
2. Die neue Transformation muß für alle Raum- und Zeitpunkte gelten.
3. Für kleine Relativgeschwindigkeiten zwischen den Bezugssystemen ( v << c ) muß die neue Transformation in die Galileitransformation (s.o.) übergehen;
4. Die neue Transformation muß unabhängig von der Bewegungsrichtung (+v oder -v) sein.
5. Die neue Transformation muß symmetrisch bezüglich der Bezugssysteme sein, d.h. es darf keine Rolle spielen welches Bezugssystem als Referenz genommen wird.
6. Die neue Transformation muß die Lichtgeschwindigkeit als Grenzgeschwindigkeit beinhalten.
Das sind die Eigenschaften der Lorentz-Transformation
Wir sollten uns jetzt daran machen sie herzuleiten.
Gleichung 1a / 1b
Gleichung 2a / 2b
Gleichung 3a / 3b
Gleichung 4
Gleichung 5a
Gleichung 5b
Die Lorentz-Transformation
Genau wie oben bei der Galileitransformation reduzieren wir unsere Überlegungen auf den Spezialfall, dass die Bewegung der beiden Bezugssysteme parallel zur x- bzw. x'-Achse verläuft.
Sie müssen zugeben, daß die oben formulierenten Eigenschaften der Transformation naheliegend und eigentlich selbstverständlich sind !
Wir gehen jetzt mal sehr mathematisch an das Problem heran.
Wir unterstellen, dass die Galilei-Transformationen:
x = x' + vt' bzw. x' = x - vt
um den Faktor k ergänzt werden müssen, damit sie die obigen Bedingungen 1. - 6. erfüllen, also:
x = k.(x' + v.t') und x' = k.(x - v.t)
und diesen Faktor "k" gilt es zu bestimmen.
Wenn wir die obigen Bedingungen auf den Faktor "k" anwenden, dann gilt:
- aus 1 folgt --> k darf nicht von der Orts.- bzw. Zeitkkordinate abhängen;
- aus 3 folgt --> für v --> 0 folgt k --> 1
- aus 4+5 folgt --> k(-v) = k(+v)
- aus 4 folgt --> k(-v) = k(+v), das könnte bedeuten, k ist eine Funktion von
- --> k muß dimensionslos sein, d.h. k ist eine Funktion von
Neben der Transformation der Ortskoordinaten (x,y,z) und (x',y',z') folgt aus dem 2.Postulat ("die Lichtgeschwindigkeit ist in jedem Bezugssystem eine Konstante), dass wir auch noch eine Transformation zwischen den Zeiten t und t' benötigen. Da sich ein Lichtsignal unabhängig von der Position des Beobachters mit der Geschwindigkeit c ausbreitet, gilt:
v = c.t und x' = c.t'
Was jetzt folgt ist eine ziemlich ermüdende, aber letztlich triviale Hin- und Herschieberei der obigen Gleichungen; ich will Ihnen diese Gleichungsakrobatik nicht vorenthalten, - aber Sie können Sie auch getrost überspringen !
zur Bestimmung des Lorentzfaktors k brauchen wir zunächst die Koordinaten-Transformationen:
x = k.(x' + v.t') x' = k.(x - v.t)
und
x = c.t x' = c.t'
durch Einsetzen von 2a / 2b in 1a / 1b ergibt sich:
c.t = k.(c.t' + v.t') c.t' = k.(c.t - v.t)
Multiplizieren von Gleichung 2a und 2b:
Nun löst man das Ganze nach dem Lorentzfaktor k auf und erhält:
Was uns jetzt noch fehlt sind die Transformationsgleichungen für die Zeit:
mit c.t = k.(c.t' + v.t') umgeformt zu t= k.(t' + v.t'/c) und x' = c.t' umgeformt zu t'=x'/v erhalten wir :
und analog:

Lassen Sie uns die Gleichungen der Lorentz-Transformation zusammenfassen:
x = k.(x' + v.t') x' = k.(x - v.t)
y = y' y' = y
z = z' z' = z
t = k.(t' + v.x'/c2) t' = k.(t + v.x/c2)
mit: und:

Sie können ja 'mal überprüfen, ob die oben genannten Eigenschaften der Lorentztransformation wirklich eingehalten werden, z.B.:
3. Für kleine Relativgeschwindigkeiten zwischen den Bezugssystemen ( v << c ) muß die neue Transformation in die Galileitransformation übergehen.
Wir nehmen 'mal an, dass die Relativgeschwindigkeit v =0 ist. Daraus folgt k = 1 und für die Koordinatentransformationen ergibt sich daraus:
x = x' + v.t'
y = y'
z = z'
t = t'
... also die ganz normale Galileitransformation ! (s.d. hier)
Darf ich Sie daran erinnern warum wir uns die Mühe mit der Lorentztransformation überhaupt gemacht haben?
--> Wir wollten die relativistische Addition von Geschwindigkeiten herleiten


Also nochmal:
- Sie stehen neben einem Wagen der - relativ zu Ihnen - mit der Geschwindigkeit v fährt.
- auf dem Wagen fährt ein zweiter Wagen mit der Geschwindigkeit u, - relativ zum ersten Wagen
- welche Geschwindigkeit w hat der zweite Wagen relativ zu Ihrer Position ?
Ganz generell wird die Geschwindigkeit w beschrieben durch
w = x / t
Wir müssen nun x und t mit Hilfe der Lorentztransformation in das Koordinastensystem x' und t' transformieren und in den Ausdruck w = x / t einsetzen:
Das ist jetzt etwas "unübersichtlich", aber wir werden es gleich vereinfachen !
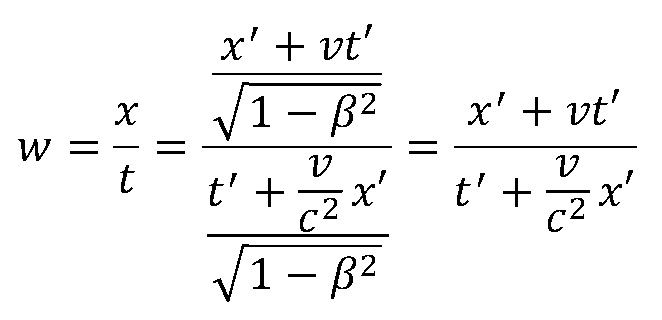
Im nächsten Schritt dividieren wir Zähler und Nenner durch t' und erhalten:

relativistische Addition von zwei Geschwindigkeiten:
x' / t' beschreibt die Geschwindigkeit u im bewegten (x',y',z',t')-System, d.h.
Daraus folgt das


relativistische Additionstheorem:
.. und damit haben wir die Beziehung, die die Addition von zwei Geschwindigkeiten u und v nach den Prinzipien der speziellen Relativitätsdtheorie beschreibt!
So, jetzt haben wir die Werkzeuge beieinander, die wir brauchen um die am Michelson- und am Sagnacinterferometer beobachteten Effekte richtig, vorallem aber widerspruchsfrei beschreiben zu können:
Das Michelson-Interferometer kann für den mitbewegten Beobachter schon wegen des klassischen Relativitätsprinzips nach Galileo Gililei keinen Laufwegeffekt zeigen, aber die relativistische Beschreibung ergibt, dass auch der ruhende Beobachter keinen Effekt registrieren kann.
Das Sagnac-Interferometer reagiert zwar auf Drehbewegungen, aber die relativistisch korrekte Beschreibung macht deutlich dass dieser Effekt vollkommen unabhängig von der Signalgeschwindigkeit ist. Diese besondere Eigenschaft des Sagnac-Interferometers qualifiziert das Gerät zum Präzisionssensor, macht aber auch deutlich, das die klassische - nicht-relativische Beschreibung falsch sein muß, denn die Formel zur Berechnung des Laufwegsdifferenz enthält zwar die Lichtgeschwindigkeit c, aber nicht als Parameter der verwendeten Lichtquelle, sondern als Naturkonstante. (als Naturkonstante gerät "c" über das realtivistische Addidtionstheorem in die Beschreibung des Ausgangssignals - die Signalgeschwindigkeit selbst fällt heraus !, s.d. Sagnac-II .)